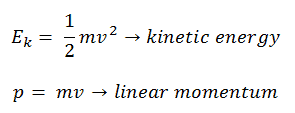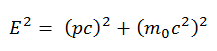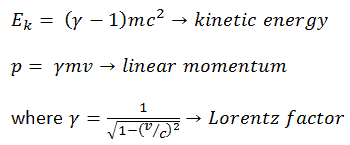Energie cinétique relativiste
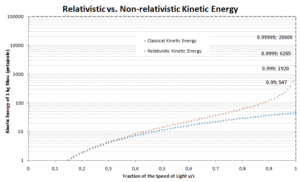
Les relations précédentes entre le travail et l’énergie cinétique sont basées sur les lois du mouvement de Newton . Lorsque nous généralisons ces lois selon le principe de relativité, nous avons besoin d’une généralisation correspondante de l’équation de l’énergie cinétique . Si la vitesse d’un objet est proche de la vitesse de la lumière, il est nécessaire d’utiliser une mécanique relativiste pour calculer son énergie cinétique .
En mécanique classique , l’énergie cinétique et la quantité de mouvement sont exprimées par:
La dérivation de ses relations relativistes est basée sur la relation relativiste énergie-impulsion:
On peut en déduire que l’énergie cinétique relativiste et l’élan relativiste sont:
Le premier terme ( mc 2 ) de l’ énergie cinétique relativiste augmente avec la vitesse v de la particule. Le second terme ( mc 2 ) est constant; elle est appelée énergie de repos (masse au repos) de la particule et représente une forme d’énergie qu’une particule possède même à une vitesse nulle . Lorsque la vitesse d’un objet s’approche de la vitesse de la lumière, l’ énergie cinétique se rapproche de l’infini . Il est causé par le facteur de Lorentz , qui approche l’infini pour v → c . Par conséquent, la vitesse de la lumière ne peut être atteinte par aucune particule massive.
Le premier terme (ɣmc 2 ) est connu comme l’ énergie totale E de la particule, car il est égal à l’énergie de repos plus l’énergie cinétique:
E = K + mc 2
Pour une particule au repos, c’est-à-dire que K est nul, l’énergie totale est donc son énergie de repos:
E = mc 2
C’est l’un des résultats frappants de la théorie de la relativité d’Einstein : la masse et l’énergie sont équivalentes et convertibles l’ une dans l’autre. L’équivalence de la masse et de l’énergie est décrite par la célèbre formule d’Einstein E = mc 2 . Ce résultat a été confirmé à maintes reprises expérimentalement en physique nucléaire et élémentaire des particules. Par exemple, voir Production de paires positrons-électrons ou Conservation de l’énergie dans les réactions nucléaires .
Voir aussi: Messe relativiste
Exemple: énergie cinétique du proton
Un proton ( m = 1,67 x 10 -27 kg ) se déplace à une vitesse v = 0,9900c = 2,968 x 10 8 m / s . Quelle est son énergie cinétique ?
Selon un calcul classique, qui n’est pas correct, on obtiendrait:
K = 1 / 2mv 2 = ½ x (1,67 x 10 -27 kg) x (2,968 x 10 8 m / s) 2 = 7,355 x 10 -11 J
Avec la correction relativiste, l’énergie cinétique relativiste est égale à:
K = (ɣ – 1) mc 2
où le facteur de Lorentz
ɣ = 7,089
par conséquent
K = 6,089 x (1,67 x 10 -27 kg) x (2,9979 x 10 8 m / s) 2 = 9,139 x 10 -10 J = 5,701 GeV
C’est environ 12 fois plus d’ énergie que dans le calcul classique. Selon cette relation, une accélération d’un faisceau de protons à 5,7 GeV nécessite des énergies qui sont dans l’ordre différent.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
