Numéro de Prandtl
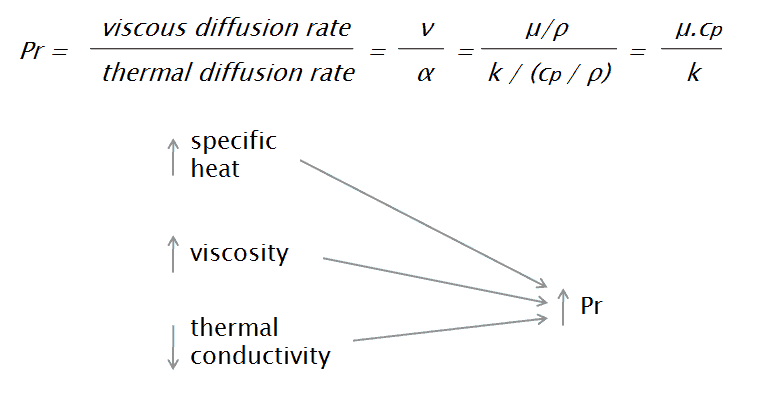
Le numéro de Prandtl est un nombre sans dimension, du nom de son inventeur, l’ingénieur allemand Ludwig Prandtl , qui a également identifié la couche limite . Le nombre de Prandtl est défini comme le rapport de la dynamique diffusivité de la diffusivité thermique . La diffusivité du moment , ou comme on l’appelle normalement, la viscosité cinématique, indique la résistance du matériau aux flux de cisaillement (différentes couches du flux se déplacent avec des vitesses différentes dues par exemple à des vitesses différentes des parois adjacentes) en relation avec la densité. C’est-à-dire que le numéro de Prandtl est donné par:
où:
ν est la diffusivité du moment (viscosité cinématique) [m 2 / s]
α est la diffusivité thermique [m 2 / s]
μ est la viscosité dynamique [Ns / m 2 ]
k est la conductivité thermique [W / mK]
c p est la chaleur spécifique [J / kg.K]
ρ est la densité [kg / m 3 ]
 De petites valeurs du nombre de Prandtl , Pr << 1 , signifient que la diffusivité thermique est prépondérante. Alors qu’avec de grandes valeurs, Pr >> 1 , la diffusivité du moment domine le comportement. Par exemple, la valeur typique pour le mercure liquide, qui est d’environ 0,025, indique que la conduction thermique est plus importante que la convection , de sorte que la diffusivité thermique est dominante. Lorsque Pr est petit, cela signifie que la chaleur diffuse rapidement par rapport à la vitesse.
De petites valeurs du nombre de Prandtl , Pr << 1 , signifient que la diffusivité thermique est prépondérante. Alors qu’avec de grandes valeurs, Pr >> 1 , la diffusivité du moment domine le comportement. Par exemple, la valeur typique pour le mercure liquide, qui est d’environ 0,025, indique que la conduction thermique est plus importante que la convection , de sorte que la diffusivité thermique est dominante. Lorsque Pr est petit, cela signifie que la chaleur diffuse rapidement par rapport à la vitesse.
Comparé au nombre de Reynolds , le nombre de Prandtl ne dépend pas de la géométrie d’un objet impliqué dans le problème, mais dépend uniquement du fluide et de son état. En tant que tel, le nombre de Prandtl se trouve souvent dans les tableaux de propriétés, aux côtés d’autres propriétés telles que la viscosité et la conductivité thermique.
Prandtl Nombre d’eau et d’air
L’air à température ambiante a un indice Prandtl de 0,71 et pour l’ eau à 18 ° C, il est d’environ 7,56 , ce qui signifie que la diffusivité thermique est plus dominante pour l’air que pour l’eau. Pour un nombre d’unités de Prandtl, la diffusivité d’impulsion est égale à la diffusivité thermique et le mécanisme et le taux de transfert de chaleur sont similaires à ceux du transfert d’impulsion. Pour de nombreux fluides, Pr est compris entre 1 et 10. Pour les gaz, Pr est généralement d’environ 0,7.
Prandtl Nombre de métaux liquides
Pour les métaux liquides, le nombre de Prandtl est très faible, généralement compris entre 0,01 et 0,001. Cela signifie que la diffusivité thermique , qui est liée au taux de transfert de chaleur par conduction , domine sans ambiguïté . Cette très grande diffusivité thermique résulte d’une très forte conductivité thermique des métaux, qui est environ 100 fois supérieure à celle de l’eau. Le nombre de Prandtl pour le sodium à une température de fonctionnement typique dans les réacteurs rapides refroidis au sodium est d’environ 0,004.
Le nombre de Prandtl entre dans de nombreux calculs de transfert de chaleur dans les réacteurs à métal liquide. Deux des modèles prometteurs de réacteurs de génération IV utilisent un métal liquide comme fluide de refroidissement du réacteur. Le développement des réacteurs de génération IV représente un défi d’un point de vue technique.
- Réacteur rapide refroidi au sodium
- Réacteur rapide refroidi au plomb
L’un des principaux défis de la simulation numérique est la modélisation fiable du transfert de chaleur dans les réacteurs refroidis au métal liquide par Computational Fluid Dynamics (CFD). Les applications de transfert de chaleur avec des fluides à faible indice de Prandtl sont souvent dans la plage de transition entre les régimes dominés par la conduction et la convection.
Numéro de Prandtl laminaire – Numéro de Prandtl turbulent
Pour les nombres de Prandtl , nous devons définir une partie laminaire du nombre de Prandtl et une partie turbulente du nombre de Prandtl. L’équation Pr = ν / α , ne nous montre en fait que la partie laminaire qui n’est valable que pour les écoulements laminaires . L’équation suivante nous montre le nombre de Prandtl effectif :
Pr eff = ν / α + ν t / α t
où ν t est la viscosité turbulente cinématique et α t est la diffusivité thermique turbulente. Le nombre turbulent de Prandtl (Pr t = ν t / α t ) est un terme non dimensionnel défini comme le rapport entre la diffusivité de tourbillon de momentum et la diffusivité de tourbillon de transfert de chaleur. Il décrit simplement le mélange à cause du tourbillonnement / rotation des fluides. Le modèle le plus simple pour Pr t est l’ analogie de Reynolds , qui donne un nombre turbulent de Prandtl de 1.
Dans le cas particulier où le nombre de Prandtl et le nombre de Prandtl turbulent sont tous deux égaux à l’unité (comme dans l’analogie de Reynolds), le profil de vitesse et les profils de température sont identiques. Cela simplifie considérablement la solution du problème de transfert de chaleur. D’après les données expérimentales, le nombre turbulent de Prandtl est d’environ 0,7 pour différentes couches de cisaillement libre, et pour les écoulements près de la paroi, il est plus grand (Pr t = 0,9) et parfois au-delà de 1 car il a tendance à croître plus près des parois.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci