O que é a fórmula do momento – Equação do momento – Definição

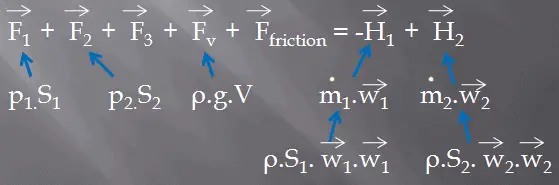
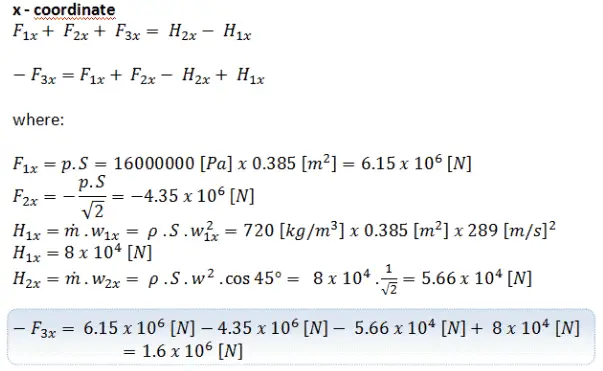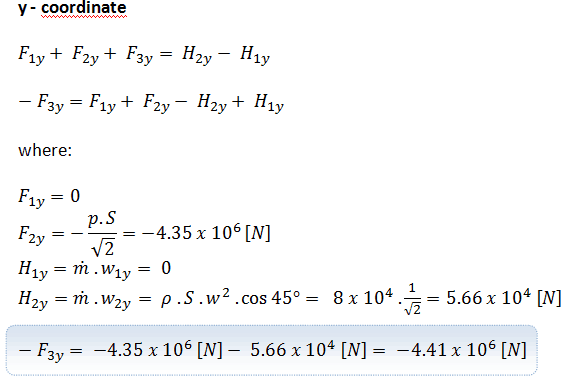Fórmula do Momento – Equação do Momento

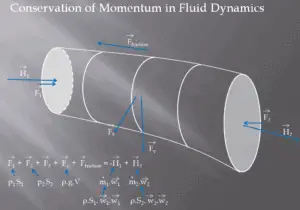Assumimos que o fluido seja estável e incompressível . Para determinar a taxa de mudança de momento de um fluido, consideraremos um tubo de fluxo ( volume de controle ), como fizemos na equação de Bernoulli . Nesse volume de controle, qualquer alteração no momento do fluido dentro de um volume de controle é devida à ação de forças externas no fluido dentro do volume.

Como pode ser visto na figura, o método do volume de controle pode ser usado para analisar a lei de conservação do momento no fluido. O volume de controle é uma superfície imaginária que encerra um volume de interesse. O volume de controle pode ser fixo ou móvel, e pode ser rígido ou deformável. Para determinar todas as forças que atuam nas superfícies do volume de controle, temos que resolver as leis de conservação nesse volume de controle.

A primeira equação de conservação que devemos considerar no volume de controle é a equação de continuidade ( a lei da conservação da massa ). Na forma mais simples, é representado pela seguinte equação:

∑ṁ _dentro = ∑ṁ _fora

Soma das taxas de fluxo de massa entrando por unidade de tempo = Soma das taxas de fluxo de massa saindo por unidade de tempo

A segunda equação de conservação que devemos considerar no volume de controle é a fórmula do momento . Na forma mais simples, a fórmula do momento pode ser representada pela seguinte equação:

–

Escolhendo um volume de controle

Um volume de controle pode ser selecionado como qualquer volume arbitrário através do qual o fluido flui. Esse volume pode ser estático, em movimento e até deformar durante o fluxo. Para resolver qualquer problema, precisamos resolver as leis básicas de conservação neste volume. É muito importante conhecer todas as velocidades de fluxo relativas à superfície de controle e, portanto, é muito importante definir exatamente os limites do volume de controle durante uma análise.

Exemplo: a força que atua sobre um cotovelo defletor

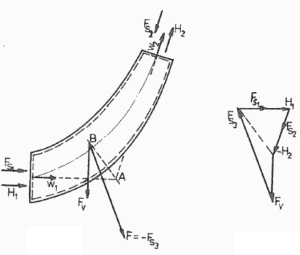Um cotovelo (digamos da tubulação primária) é usado para desviar o fluxo de água a uma velocidade de 17 m / s . O diâmetro da tubulação é igual a 700 mm . A pressão manométrica no interior do tubo é de cerca de 16 MPa à temperatura de 290 ° C. Fluido é de densidade constante ⍴ ~ 720 kg / m ³ (a 290 ° C). O ângulo do cotovelo é de 45 ° .

Calcule a força na parede de um cotovelo defletor (ou seja, calcule o vetor F ₃ ).

Premissas:

• O fluxo é constante.
• As perdas por atrito são insignificantes.
• O peso do cotovelo é insignificante.
• O peso da água no cotovelo é insignificante.

Tomamos o cotovelo como o volume de controle . O volume de controle é mostrado na imagem. A equação do momento é uma equação vetorial, portanto possui três componentes. Tomamos as coordenadas x e z como mostrado e resolveremos o problema separadamente, de acordo com essas coordenadas.

Primeiro, vamos considerar o componente na coordenada x . A conservação da equação do momento linear se torna:

Segundo, vamos considerar o componente na coordenada y . A conservação da equação do momento linear se torna:

A força final que atua na parede de um cotovelo defletor será:

Exemplo: jato de água atingindo uma placa estacionária

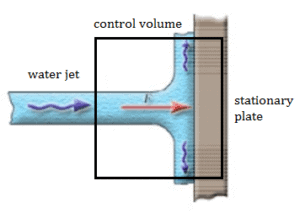Uma placa estacionária (por exemplo, lâmina de um moinho de água) é usada para desviar o fluxo de água a uma velocidade de 1 m / se a um ângulo de 90 ° . Ocorre à pressão atmosférica e a vazão mássica é igual a Q = 1 m ³ / s .

1. Calcule a força da pressão.
2. Calcule a força do corpo.
3. Calcule a força total.
4. Calcule a força resultante.

Solução

1. A força da pressão é zero, pois a pressão na entrada e nas saídas do volume de controle é atmosférica.
2. Como o volume de controle é pequeno, podemos ignorar a força do corpo devido ao peso da gravidade.
3. F _x = ρ.Q. (w _1x – w _2x ) = 1000. 1 (1 – 0) = 1000 N
   F _y = 0
   F = (1000, 0)
4. A força resultante no plano é da mesma magnitude, mas na direção oposta à força total F (atrito e peso são negligenciados).

O jato de água exerce sobre a placa a força de 1000 N na direção x.