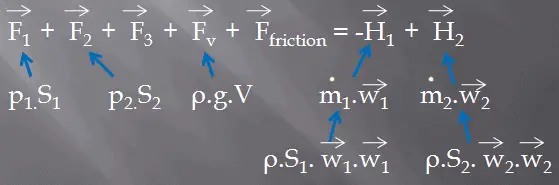
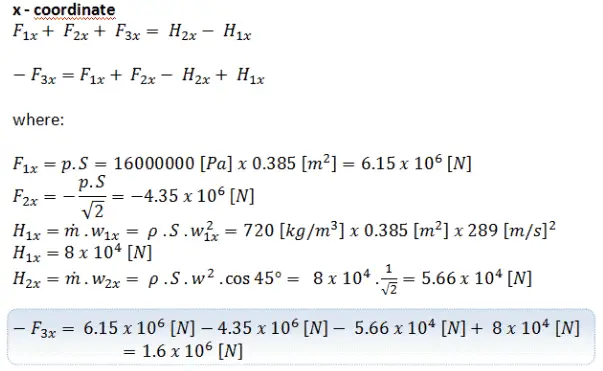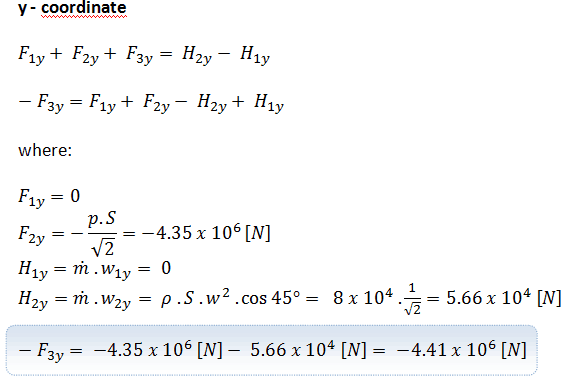Formule Momentum – Equation Momentum
Nous supposons que le fluide est à la fois régulier et incompressible . Pour déterminer le taux de changement de quantité de mouvement d’un fluide, considérons un tube de flux ( volume de contrôle ) comme nous l’avons fait pour l’ équation de Bernoulli . Dans ce volume de contrôle, toute modification de la quantité de mouvement du fluide dans un volume de contrôle est due à l’action de forces externes sur le fluide dans le volume.
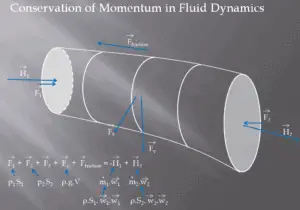
Comme on peut le voir sur l’image, la méthode du volume de contrôle peut être utilisée pour analyser la loi de conservation de la quantité de mouvement dans un fluide. Le volume de contrôle est une surface imaginaire renfermant un volume d’intérêt. Le volume de contrôle peut être fixe ou en mouvement, et il peut être rigide ou déformable. Afin de déterminer toutes les forces agissant sur les surfaces du volume de contrôle, nous devons résoudre les lois de conservation dans ce volume de contrôle.
La première équation de conservation à prendre en compte dans le volume de contrôle est l’ équation de continuité ( loi de la conservation de la matière ). Dans sa forme la plus simple, il est représenté par l’équation suivante:
∑ṁ in = ∑ṁ out
Somme des débits massiques entrant par unité de temps = Somme des débits massiques sortant par unité de temps
La deuxième équation de conservation que nous devons prendre en compte dans le volume de contrôle est la formule de quantité de mouvement . Dans la forme la plus simple, la formule d’impulsion peut être représentée par l’équation suivante:
–
Choisir un volume de contrôle
Un volume de contrôle peut être sélectionné comme n’importe quel volume arbitraire à travers lequel le fluide s’écoule. Ce volume peut être statique, en mouvement et même se déformer pendant le flux. Afin de résoudre tout problème, nous devons résoudre les lois de base sur la conservation dans ce volume. Il est très important de connaître toutes les vitesses d’écoulement relatives vers la surface de contrôle. Il est donc très important de définir avec précision les limites du volume de contrôle lors d’une analyse.
Exemple: la force agissant sur un coude déflecteur
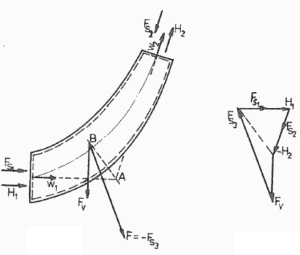Un coude (disons de la tuyauterie primaire) est utilisé pour dévier le débit d’eau à une vitesse de 17 m / s . Le diamètre de la tuyauterie est égal à 700 mm . La pression manométrique à l’intérieur du tuyau est d’environ 16 MPa à la température de 290 ° C. Le fluide est de densité constante ⍴ ~ 720 kg / m 3 (à 290 ° C). L’angle du coude est de 45 ° .
Calculer la force sur la paroi d’un coude déflecteur (c.-à-d. Calculer le vecteur F 3 ).
Hypothèses:
- Le débit est régulier.
- Les pertes par friction sont négligeables.
- Le poids du coude est négligeable.
- Le poids de l’eau dans le coude est négligeable.
Nous prenons le coude comme volume de contrôle . Le volume de contrôle est indiqué sur l’image. L’équation de quantité de mouvement est une équation vectorielle, elle a donc trois composantes. Nous prenons les coordonnées x et z comme indiqué et nous résoudrons le problème séparément en fonction de ces coordonnées.
Tout d’abord, considérons le composant dans la coordonnée x . La conservation de l’équation du moment linéaire devient:
Deuxièmement, considérons le composant dans la coordonnée y . La conservation de l’équation du moment linéaire devient:
La force finale agissant sur la paroi d’un coude déflecteur sera:
Exemple: jet d’eau frappant une plaque fixe
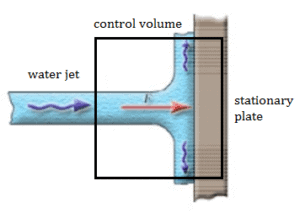Une plaque fixe (par exemple, la lame d’un moulin à eau) est utilisée pour dévier le débit d’eau à une vitesse de 1 m / s et à un angle de 90 ° . Il se produit à la pression atmosphérique et le débit massique est égal à Q = 1 m 3 / s .
- Calculez la force de pression.
- Calculez la force corporelle.
- Calculez la force totale.
- Calculez la force résultante.
Solution
- La force de pression est nulle car la pression à l’entrée et à la sortie du volume de contrôle est atmosphérique.
- Comme le volume de contrôle est petit, nous pouvons ignorer la force corporelle due au poids de la gravité.
- F x = ρ.Q. (w 1x – w 2x ) = 1000. 1 . (1 – 0) = 1000 N
F y = 0
F = (1000, 0) - La force résultante sur le plan est de la même amplitude mais dans le sens opposé à la force totale F (le frottement et le poids sont négligés).
Le jet d’eau exerce sur la plaque la force de 1000 N dans la direction x.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
