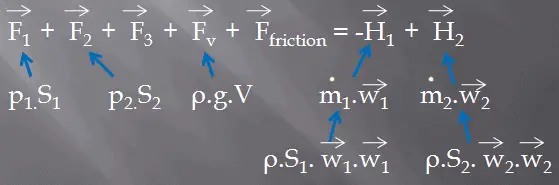
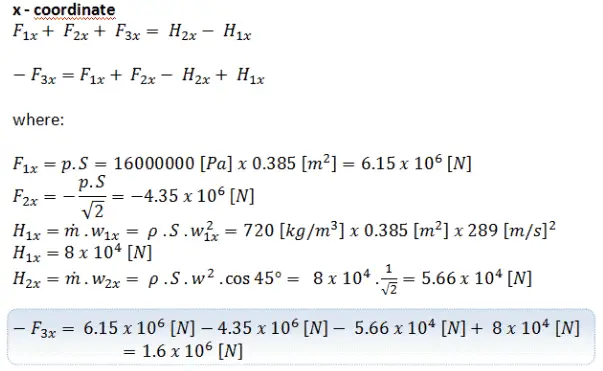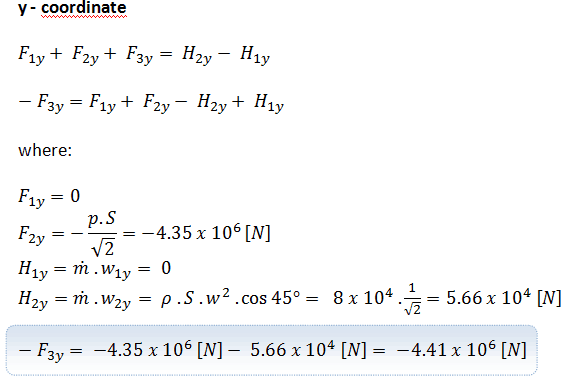Fórmula Momentum – Ecuación Momentum
 Asumimos que el fluido es estable e incompresible . Para determinar la tasa de cambio de momento para un fluido, consideraremos un tubo de flujo ( volumen de control ) como lo hicimos para la ecuación de Bernoulli . En este volumen de control, cualquier cambio en el momento del fluido dentro de un volumen de control se debe a la acción de fuerzas externas sobre el fluido dentro del volumen.
Asumimos que el fluido es estable e incompresible . Para determinar la tasa de cambio de momento para un fluido, consideraremos un tubo de flujo ( volumen de control ) como lo hicimos para la ecuación de Bernoulli . En este volumen de control, cualquier cambio en el momento del fluido dentro de un volumen de control se debe a la acción de fuerzas externas sobre el fluido dentro del volumen.
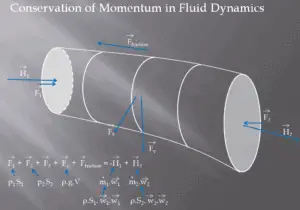
Como se puede ver en la imagen, el método de control de volumen puede usarse para analizar la ley de conservación del momento en el fluido. El volumen de control es una superficie imaginaria que encierra un volumen de interés. El volumen de control puede ser fijo o en movimiento, y puede ser rígido o deformable. Para determinar todas las fuerzas que actúan sobre las superficies del volumen de control, tenemos que resolver las leyes de conservación en este volumen de control.
La primera ecuación de conservación que tenemos que considerar en el volumen de control es la ecuación de continuidad ( la ley de conservación de la materia ). En la forma más simple se representa mediante la siguiente ecuación:
∑ṁ dentro = ∑ṁ fuera
Suma de caudales másicos entrantes por unidad de tiempo = Suma de caudales másicos que salen por unidad de tiempo
La segunda ecuación de conservación que debemos considerar en el volumen de control es la fórmula de impulso . En la forma más simple, la fórmula de impulso puede representarse mediante la siguiente ecuación:
Elegir un volumen de control
Se puede seleccionar un volumen de control como cualquier volumen arbitrario a través del cual fluye el fluido. Este volumen puede ser estático, en movimiento e incluso deformarse durante el flujo. Para resolver cualquier problema, tenemos que resolver las leyes básicas de conservación en este volumen. Es muy importante conocer todas las velocidades de flujo relativas a la superficie de control y, por lo tanto, es muy importante definir exactamente los límites del volumen de control durante un análisis.
Ejemplo: la fuerza que actúa sobre un codo deflector
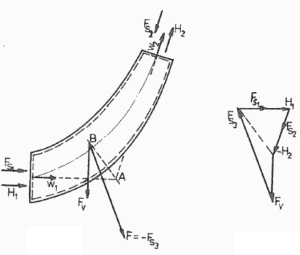 Se utiliza un codo (digamos de la tubería primaria) para desviar el flujo de agua a una velocidad de 17 m / s . El diámetro de la tubería es igual a 700 mm . La presión manométrica dentro de la tubería es de aproximadamente 16 MPa a una temperatura de 290 ° C. El fluido tiene una densidad constante ⍴ ~ 720 kg / m 3 (a 290 ° C). El ángulo del codo es de 45 ° .
Se utiliza un codo (digamos de la tubería primaria) para desviar el flujo de agua a una velocidad de 17 m / s . El diámetro de la tubería es igual a 700 mm . La presión manométrica dentro de la tubería es de aproximadamente 16 MPa a una temperatura de 290 ° C. El fluido tiene una densidad constante ⍴ ~ 720 kg / m 3 (a 290 ° C). El ángulo del codo es de 45 ° .
Calcule la fuerza en la pared de un codo deflector (es decir, calcule el vector F 3 ).
Suposiciones
- El flujo es constante.
- Las pérdidas por fricción son insignificantes.
- El peso del codo es insignificante.
- El peso del agua en el codo es insignificante.
Tomamos el codo como el volumen de control . El volumen de control se muestra en la imagen. La ecuación de momento es una ecuación vectorial, por lo que tiene tres componentes. Tomamos las coordenadas x y z como se muestra y resolveremos el problema por separado de acuerdo con estas coordenadas.
Primero, consideremos el componente en la coordenada x . La conservación de la ecuación de momento lineal se convierte en:
Segundo, consideremos el componente en la coordenada y . La conservación de la ecuación de momento lineal se convierte en:
La fuerza final que actúa sobre la pared de un codo deflector será:
Ejemplo: chorro de agua golpeando una placa estacionaria
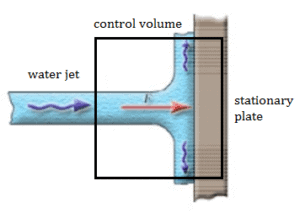 Se utiliza una placa estacionaria (por ejemplo, la cuchilla de un molino de agua) para desviar el flujo de agua a una velocidad de 1 m / sy en un ángulo de 90 ° . Ocurre a presión atmosférica y el caudal másico es igual a Q = 1 m 3 / s .
Se utiliza una placa estacionaria (por ejemplo, la cuchilla de un molino de agua) para desviar el flujo de agua a una velocidad de 1 m / sy en un ángulo de 90 ° . Ocurre a presión atmosférica y el caudal másico es igual a Q = 1 m 3 / s .
- Calcule la fuerza de presión.
- Calcule la fuerza del cuerpo.
- Calcule la fuerza total.
- Calcule la fuerza resultante.
Solución
- La fuerza de presión es cero ya que la presión tanto en la entrada como en las salidas al volumen de control es atmosférica.
- Como el volumen de control es pequeño, podemos ignorar la fuerza del cuerpo debido al peso de la gravedad.
- F x = ρ.Q. (w 1x – w 2x ) = 1000. 1) (1-0) = 1000 N
F y = 0
F = (1000, 0) - La fuerza resultante en el plano es de la misma magnitud pero en la dirección opuesta a la fuerza total F (se desprecian la fricción y el peso).
El chorro de agua ejerce sobre la placa la fuerza de 1000 N en la dirección x.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.