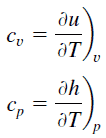Lei dos gases ideais

O modelo de gás ideal é baseado nas seguintes suposições:

1. A pressão, o volume e a temperatura de um gás ideal obedecem à lei do gás ideal .
2. A energia interna específica é apenas uma função da temperatura: u = u (T)
3. A massa molar de um gás ideal é idêntica à massa molar da substância real
4. Os aquecimentos específicos – c _p e c _v – são independentes da temperatura, o que significa que são constantes.

Do ponto de vista microscópico, é baseado nas seguintes premissas:

1. As moléculas do gás são pequenas esferas duras .
2. As únicas forças entre as moléculas de gás são aquelas que determinam as colisões pontuais .
3. Todas as colisões são elásticas e todo movimento é sem atrito .
4. A distância média entre as moléculas é muito maior que o tamanho das moléculas.
5. As moléculas estão se movendo em direções aleatórias.
6. Não há outra força atraente ou repulsiva entre essas moléculas.

Segunda Lei de Joule

Para qualquer gás cuja equação de estado seja dada exatamente por pV = nRT (ou pv = RT ), a energia interna específica depende apenas da temperatura. Essa regra foi encontrada originalmente em 1843 pelo físico inglês James Prescott Joule experimentalmente para gases reais e é conhecida como segunda lei de Joule :

A energia interna de uma massa fixa de um gás ideal depende apenas de sua temperatura (não pressão ou volume).

A entalpia específica de um gás descrita por pV = nRT também depende apenas da temperatura. Observe que a entalpia é a quantidade termodinâmica equivalente ao conteúdo total de calor de um sistema. É igual à energia interna do sistema mais o produto de pressão e volume. Em variáveis ​​intensivas, a segunda lei de Joule é dada por h = h (T) = u (T) + pv = u (T) + RT.

Essas três equações constituem o modelo de gás ideal, resumido da seguinte forma:

pv = RT

u = u (T)

h = h (T) = u (T) + RT

Lei do gás ideal

Qualquer equação que relacione a pressão, a temperatura e o volume específico de uma substância é chamada de equação de estado . A equação de estado mais simples e mais conhecida para substâncias na fase gasosa é a equação de estado do gás ideal . Foi declarado pela primeira vez por Émile Clapeyron em 1834 como uma combinação da lei empírica de Boyle, da lei de Charles e da lei de Avogadro. Esta equação prevê o comportamento pvT de um gás com bastante precisão para gases diluídos ou de baixa pressão. Num gás ideal, as moléculas não têm volume e não interagem. De acordo com a lei ideal dos gases, a pressão varia linearmente com a temperatura e a quantidade e inversamente com o volume .

pV = nRT

Onde:

• p é a pressão absoluta do gás
• n é a quantidade de substância
• T é a temperatura absoluta
• V é o volume
• R  é a constante de gás ideal, ou universal,igual ao produto da constante de Boltzmann e da constante de Avogadro,

Nesta equação, o símbolo R é uma constante chamada constante universal de gás que tem o mesmo valor para todos os gases – ou seja, R = 8,31 J / mol K.

O poder da lei do gás ideal está em sua simplicidade . Quando quaisquer duas das variáveis ​​termodinâmicas, p, ve T são dadas , a terceira pode ser facilmente encontrada . Muitas condições físicas dos gases calculadas pelos engenheiros se enquadram na descrição acima. Talvez o uso mais comum do comportamento do gás estudado pelos engenheiros seja o processo de compressão e expansão usando aproximações ideais de gás.

Leis do gás

Em geral, as leis dos gases são as primeiras equações de estado , que correlacionam densidades de gases e líquidos a temperaturas e pressões. As leis de gás foram completamente desenvolvidas no final do século XVIII. Essas leis ou declarações precederam a lei do gás ideal , pois individualmente essas leis são consideradas casos especiais da equação do gás ideal, com uma ou mais variáveis ​​mantidas constantes. Como eles foram quase completamente substituídos pela equação ideal dos gases, não é comum os alunos aprenderem essas leis em detalhes. A equação do gás ideal foi declarada pela primeira vez por Émile Clapeyron em 1834 como uma combinação dessas leis:

• Lei de Boyle-Mariotte
• Lei de Charles
• Lei de Guy-Lussac
• Lei de Avogadro

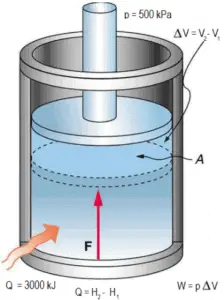
Exemplo: Lei do gás ideal – Compressão de gás dentro de um pressurizador

A pressão no circuito primário dos PWRs é mantida por um pressurizador , um vaso separado que é conectado ao circuito primário (perna quente) e parcialmente preenchido com água que é aquecida até a temperatura de saturação (ponto de ebulição) para a pressão desejada por energia elétrica submersa. aquecedores . Durante o aquecimento da planta, o pressurizador pode ser preenchido com nitrogênio, em vez de vapor saturado .

Suponha que um pressurizador contenha 12 m ³ de nitrogênio a 20 ° C e 15 bar . A temperatura é aumentada para 35 ° C e o volume é reduzido para 8,5 m ³ . Qual é a pressão final do gás dentro do pressurizador? Suponha que o gás seja ideal.

Solução:

Como o gás é ideal, podemos usar a lei do gás ideal para relacionar seus parâmetros, tanto no estado inicial ie no estado final f . Portanto:

p _init V _init = nRT _init

e

p _final V _final = nRT _final

Dividindo a segunda equação pela primeira e resolvendo para p _f , obtemos:

p _definitiva = p _Init T _definitiva V _Init / T _{o init} V _definitiva

Observe que não podemos converter unidades de volume e pressão em unidades básicas de SI, porque elas se cancelam. Por outro lado, temos que usar Kelvins em vez de graus Celsius. Portanto, T _init = 293 K e T _final = 308 K.

A seguir, a pressão resultante no estado final será:

p _final = (15 bar) x (308 K) x (12 m ³ ) / (293 K) x (8,5 m ³ ) = 22 bar

Validade da lei do gás ideal

Como o gás ideal é definido como aquele em que todas as colisões entre átomos ou moléculas são perfeitamente elásticas e nas quais não há forças de atração intermoleculares, não existe na natureza algo como um gás verdadeiramente ideal. Por outro lado, todos os gases reais se aproximam do estado ideal a baixas pressões (densidades) . A baixas pressões, as moléculas estão suficientemente afastadas para não interagirem umas com as outras.

Em outras palavras, a Lei do Gás Ideal é precisa apenas em pressões relativamente baixas (em relação à pressão crítica p _cr ) e em altas temperaturas (em relação à temperatura crítica T _cr ). Nesses parâmetros, o fator de compressibilidade, Z = pv / RT , é de aproximadamente 1 . O fator de compressibilidade é usado para explicar o desvio da situação ideal. Esse fator de correção depende da pressão e temperatura para cada gás considerado.

Energia interna de um gás ideal

A energia interna é o total de toda a energia associada ao movimento dos átomos ou moléculas no sistema. As formas microscópicas de energia incluem aquelas devidas à rotação , vibração , tradução e interações entre as moléculas de uma substância.

Gás Monatômico – Energia Interna

Para um gás ideal monatômico (como hélio, néon ou argônio), a única contribuição para a energia vem da energia cinética translacional . A energia cinética translacional média de um único átomo depende apenas da temperatura do gás e é dada pela equação:

K _méd = 3/2 kT.

A energia interna de n moles de um gás monatômico ideal (um átomo por molécula) é igual à energia cinética média por molécula vezes o número total de moléculas, N:

E _int = 3/2 NkT = 3/2 nRT

onde n é o número de moles. Cada direção (x, ye z) contribui (1/2) nRT para a energia interna . É aqui que entra a idéia da equipartição de energia – qualquer outra contribuição para a energia também deve contribuir (1/2) nRT . Como pode ser visto, a energia interna de um gás ideal depende apenas da temperatura e do número de mols de gás.

Molécula Diatômica – Energia Interna

Se as moléculas de gás contêm mais de um átomo, existem três direções de translação e a energia cinética rotacional também contribui, mas apenas para rotações em torno de dois dos três eixos perpendiculares. As cinco contribuições para a energia (cinco graus de liberdade) fornecem:

Gás ideal diatômico:

E _int = 5/2 NkT = 5/2 nRT

Esta é apenas uma aproximação e se aplica a temperaturas intermediárias. Em baixas temperaturas, apenas a energia cinética translacional contribui e, em temperaturas mais altas, duas contribuições adicionais (energia cinética e potencial) vêm da vibração. A energia interna será maior a uma determinada temperatura do que para um gás monatômico, mas ainda será uma função apenas da temperatura para um gás ideal.

A energia interna dos gases reais também depende principalmente da temperatura, mas, da mesma forma que a Lei do Gás Ideal , a energia interna dos gases reais também depende um pouco da pressão e do volume . Todos os gases reais se aproximam do estado ideal a baixas pressões (densidades). A baixas pressões, as moléculas estão suficientemente afastadas para não interagirem umas com as outras. A energia interna de líquidos e sólidos é bastante complicada, pois inclui energia potencial elétrica associada às forças (ou ligações químicas ) entre átomos e moléculas.

Calor específico a volume constante e pressão constante

O calor específico é uma propriedade relacionada à energia interna que é muito importante na termodinâmica. As propriedades intensivas c _v e c _p são definidas para substâncias compressíveis puras e simples como derivados parciais da energia interna u (T, v) e entalpia h (T, p) , respectivamente:

onde os subscritos v e p denotam as variáveis ​​mantidas fixas durante a diferenciação. As propriedades c _v e c _p são referidos como calores específicos (ou capacidades de calor ), porque, sob determinadas condições especiais dizem respeito a mudança de temperatura de um sistema para a quantidade de energia adicionada pela transferência de calor. As suas unidades SI são J / kg K ou J / mol K . Dois aquecimentos específicos são definidos para gases, um para volume constante (c _v ) e outro para pressão constante (c _p ) .

De acordo com a primeira lei da termodinâmica , para processos de volume constante com um gás ideal monatômico, o calor molar específico será:

C _v = 3 / 2R = 12,5 J / mol K

Porque

U = 3 / 2nRT

Pode-se derivar que o calor molar específico a pressão constante é:

C _p = C _v + R = 5 / 2R = 20,8 J / mol K

Este C _p é maior do que o calor específico molar a volume constante C _v , porque a energia deve agora ser fornecidos não só para aumentar a temperatura do gás, mas também para o gás de trabalho para fazer porque neste volume caso alterações.

Relação de Mayer – fórmula de Mayer

Julius Robert Mayer, químico e físico alemão, derivou uma relação entre o calor específico a pressão constante e o calor específico em volume constante para um gás ideal. Ele estudou o fato de que a capacidade térmica específica de um gás a pressão constante ( _Cp ) é ligeiramente maior que a volume constante ( _Cv ). Ele argumentou que esta C _p é maior do que o calor específico molar a volume constante C _v , porque a energia deve agora ser fornecidos não só para elevar a temperatura do gás, mas também para o gás para fazer o trabalho , porque neste volume caso mudanças. De acordo comNa relação de Mayer ou na fórmula de Mayer, a diferença entre essas duas capacidades de calor é igual à constante universal de gás, portanto o calor específico do molar a pressão constante é igual:

C _p = C _v + R