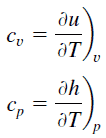Was ist das ideale Gasgesetz – Definition

Das ideale Gasmodell basiert auf folgenden Annahmen:

1. Der Druck, das Volumen und die Temperatur eines idealen Gases entsprechen dem idealen Gasgesetz .
2. Die spezifische innere Energie ist nur eine Funktion der Temperatur: u = u (T)
3. Die Molmasse eines idealen Gases ist identisch mit der Molmasse der realen Substanz
4. Die spezifischen Erhitzungen – c _p und c _v – sind unabhängig von der Temperatur, was bedeutet, dass sie Konstanten sind.

Aus mikroskopischer Sicht basiert es auf folgenden Annahmen:

1. Die Moleküle des Gases sind kleine, harte Kugeln .
2. Die einzigen Kräfte zwischen den Gasmolekülen sind diejenigen, die die punktförmigen Kollisionen bestimmen .
3. Alle Kollisionen sind elastisch und jede Bewegung ist reibungslos .
4. Der durchschnittliche Abstand zwischen Molekülen ist viel größer als die Größe der Moleküle.
5. Die Moleküle bewegen sich in zufällige Richtungen.
6. Es gibt keine andere anziehende oder abstoßende Kraft zwischen diesen Molekülen.

Joules zweites Gesetz

Für jedes Gas, dessen Zustandsgleichung genau durch pV = nRT (oder pv = RT ) gegeben ist, hängt die spezifische innere Energie nur von der Temperatur ab. Diese Regel wurde ursprünglich 1843 von einem englischen Physiker, James Prescott Joule, experimentell für echte Gase gefunden und ist als Joules zweites Gesetz bekannt :

Die innere Energie einer festen Masse eines idealen Gases hängt nur von seiner Temperatur ab (nicht von Druck oder Volumen).

Die durch pV = nRT beschriebene spezifische Enthalpie eines Gases hängt ebenfalls nur von der Temperatur ab. Beachten Sie, dass die Enthalpie die thermodynamische Größe ist, die dem Gesamtwärmegehalt eines Systems entspricht. Sie entspricht der inneren Energie des Systems plus dem Produkt aus Druck und Volumen. In intensiven Variablen ist das zweite Gesetz von Joule daher gegeben durch h = h (T) = u (T) + pv = u (T) + RT.

Diese drei Gleichungen bilden das ideale Gasmodell, zusammengefasst wie folgt:

pv = RT

u = u (T)

h = h (T) = u (T) + RT

Ideales Gasgesetz

Jede Gleichung, die den Druck, die Temperatur und das spezifische Volumen einer Substanz in Beziehung setzt, wird als Zustandsgleichung bezeichnet . Die einfachste und bekannteste Zustandsgleichung für Substanzen in der Gasphase ist die ideale Gaszustandsgleichung . Es wurde erstmals 1834 von Émile Clapeyron als eine Kombination aus dem empirischen Boyle-Gesetz, dem Charles-Gesetz und dem Avogadro-Gesetz angegeben. Diese Gleichung sagt das pvT-Verhalten eines Gases für verdünnte Gase oder Niederdruckgase ziemlich genau voraus . In einem idealen Gas haben Moleküle kein Volumen und interagieren nicht. Nach dem idealen Gasgesetz ändert sich der Druck linear mit Temperatur und Menge und umgekehrt mit dem Volumen .

pV = nRT

wo:

• p ist der absolute Druck des Gases
• n ist die Menge der Substanz
• T ist die absolute Temperatur
• V ist die Lautstärke
• R  ist die ideale oder universelle Gaskonstante , die dem Produkt der Boltzmann-Konstante und der Avogadro-Konstante entspricht.

In dieser Gleichung ist das Symbol R eine Konstante, die als universelle Gaskonstante bezeichnet wird und für alle Gase den gleichen Wert hat, nämlich R = 8,31 J / mol K.

Die Kraft des idealen Gasgesetzes liegt in seiner Einfachheit . Wenn eine beliebige zwei der thermodynamischen Variablen, p, v und T sind gegeben , das dritte kann leicht gefunden werden . Viele von Ingenieuren berechnete physikalische Bedingungen von Gasen entsprechen der obigen Beschreibung. Die wahrscheinlich häufigste von Ingenieuren untersuchte Verwendung des Gasverhaltens ist die des Kompressions- und Expansionsprozesses unter Verwendung idealer Gasnäherungen.

Gasgesetze

Im allgemeinen ist die Gasgesetze sind erste Zustandsgleichungen , das Korrelat Dichten von Gasen und Flüssigkeiten auf Temperaturen und Drücken. Die Gasgesetze wurden Ende des 18. Jahrhunderts vollständig entwickelt. Diese Gesetze oder Aussagen gingen dem idealen Gasgesetz voraus , da diese Gesetze einzeln als Sonderfälle der idealen Gasgleichung betrachtet werden, wobei eine oder mehrere der Variablen konstant gehalten werden. Da sie fast vollständig durch die ideale Gasgleichung ersetzt wurden, ist es für Schüler nicht üblich, diese Gesetze im Detail zu lernen. Die ideale Gasgleichung wurde erstmals 1834 von Émile Clapeyron als Kombination dieser Gesetze angegeben:

• Boyle-Mariotte-Gesetz
• Charles ‘Gesetz
• Guy-Lussacs Gesetz
• Avogadros Gesetz

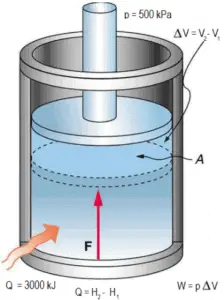
Beispiel: Ideales Gasgesetz – Gaskompression in einem Druckgerät

Der Druck im Primärkreislauf von PWRs wird durch einen Druckbeaufschlagungsapparat aufrechterhalten , ein separates Gefäß, das mit dem Primärkreislauf (heißer Zweig) verbunden und teilweise mit Wasser gefüllt ist, das durch Eintauchen in Elektrizität auf die Sättigungstemperatur (Siedepunkt) für den gewünschten Druck erhitzt wird Heizungen . Während des Aufheizens der Anlage kann der Druckbeaufschlager anstelle von Sattdampf mit Stickstoff gefüllt werden .

Angenommen, ein Druckbeaufschlagter enthält 12 m ³ Stickstoff bei 20 ° C und 15 bar . Die Temperatur wird auf 35 ° C erhöht und das Volumen auf 8,5 m ³ reduziert . Was ist der Enddruck des Gases im Druckbeauftragten? Angenommen, das Gas ist ideal.

Lösung:

Da das Gas ideal ist, können wir das ideale Gasgesetz verwenden, um seine Parameter sowohl im Anfangszustand i als auch im Endzustand f in Beziehung zu setzen . Deshalb:

p _init V _init = nRT _init

und

p _final V _final = nRT _final

Wenn wir die zweite Gleichung durch die erste Gleichung teilen und nach p _f auflösen, erhalten wir:

p _final = p _init T _final V _init / T _init V _final

Beachten Sie, dass wir Volumen- und Druckeinheiten nicht in SI-Basiseinheiten umrechnen können, da sie sich gegenseitig aufheben. Auf der anderen Seite müssen wir Kelvin anstelle von Grad Celsius verwenden. Daher ist T _init = 293 K und T _final = 308 K.

Daraus folgt, dass der resultierende Druck im Endzustand sein wird:

p _final = (15 bar) x (308 K) x (12 m ³ ) / (293 K) x (8,5 m ³ ) = 22 bar

Gültigkeit des idealen Gasgesetzes

Da ideales Gas als eines definiert ist, bei dem alle Kollisionen zwischen Atomen oder Molekülen vollkommen elastisch sind und bei dem es keine intermolekularen Anziehungskräfte gibt, gibt es in der Natur kein wirklich ideales Gas. Andererseits nähern sich alle realen Gase bei niedrigen Drücken (Dichten) dem Idealzustand an . Bei niedrigen Drücken sind Moleküle weit genug voneinander entfernt, dass sie nicht miteinander interagieren.

Mit anderen Worten ist das ideale Gasgesetz nur bei relativ niedrigen Drücken (relativ zum kritischen Druck p _cr ) und hohen Temperaturen (relativ zur kritischen Temperatur T _cr ) genau . Bei diesen Parametern beträgt der Kompressibilitätsfaktor Z = pv / RT ungefähr 1 . Der Kompressibilitätsfaktor wird verwendet, um Abweichungen von der idealen Situation zu berücksichtigen. Dieser Korrekturfaktor ist abhängig von Druck und Temperatur für jedes betrachtete Gas.

Innere Energie eines idealen Gases

Die innere Energie ist die Summe aller Energie, die mit der Bewegung der Atome oder Moleküle im System verbunden ist. Mikroskopische Energieformen umfassen solche, die auf Rotation , Vibration , Translation und Wechselwirkungen zwischen den Molekülen einer Substanz zurückzuführen sind.

Monatomisches Gas – Innere Energie

Für ein einatomiges ideales Gas (wie Helium, Neon oder Argon) kommt der einzige Beitrag zur Energie von der translatorischen kinetischen Energie . Die durchschnittliche translatorische kinetische Energie eines einzelnen Atoms hängt nur von der Gastemperatur ab und ist gegeben durch Gleichung:

K _avg = 3/2 kT.

Die innere Energie von n Mol eines idealen einatomigen Gases (ein Atom pro Molekül) entspricht der durchschnittlichen kinetischen Energie pro Molekül multipliziert mit der Gesamtzahl der Moleküle, N:

E _int = 3/2 NkT = 3/2 nRT

Dabei ist n die Anzahl der Mol. Jede Richtung (x, y und z) trägt (1/2) nRT zur inneren Energie bei . Hier kommt die Aufteilung der Energieidee ins Spiel – jeder andere Beitrag zur Energie muss ebenfalls (1/2) nRT beitragen . Wie zu sehen ist, hängt die innere Energie eines idealen Gases nur von der Temperatur und der Anzahl der Mol Gas ab.

Diatomeenmolekül – innere Energie

Wenn die Gasmoleküle mehr als ein Atom enthalten, gibt es drei Translationsrichtungen , und die kinetische Rotationsenergie trägt ebenfalls dazu bei, jedoch nur für Rotationen um zwei der drei senkrechten Achsen. Die fünf Beiträge zur Energie (fünf Freiheitsgrade) ergeben:

Diatomeen-Idealgas:

E _int = 5/2 NkT = 5/2 nRT

Dies ist nur eine Annäherung und gilt bei Zwischentemperaturen. Bei niedrigen Temperaturen trägt nur die translatorische kinetische Energie bei , und bei höheren Temperaturen kommen zwei zusätzliche Beiträge (kinetische und potentielle Energie) durch Vibration. Die innere Energie ist bei einer gegebenen Temperatur größer als bei einem einatomigen Gas, aber sie ist immer noch nur eine Funktion der Temperatur für ein ideales Gas.

Die innere Energie realer Gase hängt ebenfalls hauptsächlich von der Temperatur ab, aber ähnlich wie das ideale Gasgesetz hängt die innere Energie realer Gase auch etwas von Druck und Volumen ab . Alle realen Gase nähern sich bei niedrigen Drücken (Dichten) dem Idealzustand. Bei niedrigen Drücken sind Moleküle weit genug voneinander entfernt, dass sie nicht miteinander interagieren. Die innere Energie von Flüssigkeiten und Festkörpern ist ziemlich kompliziert, da sie elektrische potentielle Energie enthält, die mit den Kräften (oder chemischen Bindungen ) zwischen Atomen und Molekülen verbunden ist.

Spezifische Wärme bei konstantem Volumen und konstantem Druck

Spezifische Wärme ist eine Eigenschaft in Bezug auf die innere Energie , die für die Thermodynamik sehr wichtig ist. Die intensiven Eigenschaften c _v und c _p sind für reine, einfache kompressible Substanzen als partielle Ableitungen der inneren Energie u (T, v) bzw. der Enthalpie h (T, p) definiert :

wobei die Indizes v und p die Variablen bezeichnen, die während der Differenzierung festgehalten werden. Die Eigenschaften c _v und c _p werden als spezifische Wärme (oder Wärmekapazität ) bezeichnet, da sie unter bestimmten besonderen Bedingungen die Temperaturänderung eines Systems mit der durch Wärmeübertragung hinzugefügten Energiemenge in Beziehung setzen. Ihre SI – Einheiten sind J / kg K oder J / mol K . Für Gase sind zwei spezifische Wärmemengen definiert, eine für konstantes Volumen (c _v ) und eine für konstanten Druck (c _p ) .

Nach dem ersten Hauptsatz der Thermodynamik beträgt für einen Prozess mit konstantem Volumen mit einem einatomigen idealen Gas die molare spezifische Wärme:

C _v = 3 / 2R = 12,5 J / mol K.

da

U = 3 / 2nRT

Es kann abgeleitet werden, dass die molare spezifische Wärme bei konstantem Druck ist:

C _p = C _v + R = 5 / 2R = 20,8 J / mol K.

Dieses C _p ist größer als die molare spezifische Wärme bei konstantem Volumen C _v , da nun nicht nur Energie zugeführt werden muss , um die Temperatur des Gases zu erhöhen, sondern auch, damit das Gas funktioniert, da sich in diesem Fall das Volumen ändert.

Mayers Beziehung – Mayers Formel

Julius Robert Mayer, ein deutscher Chemiker und Physiker, leitete einen Zusammenhang zwischen der spezifischen Wärme bei konstantem Druck und der spezifischen Wärme bei konstantem Volumen für ein ideales Gas ab. Er untersuchte die Tatsache, dass die spezifische Wärmekapazität eines Gases bei konstantem Druck (C _p ) geringfügig größer ist als bei konstantem Volumen (C _v ). Er argumentierte, dass dieses C _p größer ist als die molare spezifische Wärme bei konstantem Volumen C _v , da nun nicht nur Energie zugeführt werden muss , um die Temperatur des Gases zu erhöhen, sondern auch, damit das Gas funktioniert, da sich in diesem Fall das Volumen ändert. Laut demMayers Beziehung oder die Mayer-Formel Die Differenz zwischen diesen beiden Wärmekapazitäten ist gleich der universellen Gaskonstante, daher ist die molare spezifische Wärme bei konstantem Druck gleich:

C _p = C _v + R.