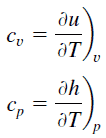Modèle de gaz parfait
Le modèle de gaz parfait est utilisé pour prédire le comportement des gaz et constitue l’un des modèles de substances les plus utiles et les plus couramment utilisés jamais développés. On m’a découvert que, si nous confinons des échantillons d’une mole de divers gaz dans un volume identique et les maintenons à la même température , leurs pressions mesurées sont presque identiques . De plus, lorsque nous confinons des gaz à des densités inférieures, les différences ont tendance à disparaître. Il a été constaté que ces gaz ont tendance à obéir à la relation suivante, appelée loi des gaz parfaits :
pV = nRT
où:
p est la pression absolue du gaz
n est la quantité de substance
T est la température absolue
Vest le volume
R est la constante de gaz idéale ou universelle,égale au produit de la constante de Boltzmann et de la constante d’Avogadro. La puissance de la loi des gaz parfaits réside dans sa simplicité. Lorsque deux des variables thermodynamiques , p, v et T, sont données, la troisième peut facilement être trouvée.
Le modèle de gaz parfait est basé sur les hypothèses suivantes:
- La pression, le volume et la température d’un gaz parfait obéissent à la loi du gaz parfait .
- L’ énergie interne spécifique est uniquement fonction de la température: u = u (T)
- La masse molaire d’un gaz parfait est identique à la masse molaire de la substance réelle
- Les chaleurs spécifiques – c p et c v – sont indépendantes de la température ce qui signifie qu’elles sont constantes.
Du point de vue microscopique, il est basé sur ces hypothèses:
- Les molécules du gaz sont de petites sphères dures .
- Les seules forces entre les molécules de gaz sont celles qui déterminent les collisions ponctuelles .
- Toutes les collisions sont élastiques et tout mouvement est sans friction .
- La distance moyenne entre les molécules est beaucoup plus grande que la taille des molécules.
- Les molécules se déplacent dans des directions aléatoires.
- Il n’y a pas d’autre force d’attraction ou de répulsion entre ces molécules.
Qu’est-ce qu’un gaz parfait
Un gaz parfait est défini comme celui dans lequel toutes les collisions entre atomes ou molécules sont parfaitement élastiques et où il n’y a pas de forces d’attraction intermoléculaires . Un gaz parfait peut être visualisé comme une collection de sphères parfaitement dures qui entrent en collision mais qui, autrement, n’interagissent pas entre elles. En réalité, aucun gaz réel n’est comme un gaz parfait et donc aucun gaz réel ne suit complètement la loi ou l’équation du gaz parfait . À des températures proches d’un point d’ébullition des gaz , augmentation de la pressionprovoquera la condensation et des baisses drastiques de volume. A des pressions très élevées, les forces intermoléculaires d’un gaz sont importantes. Cependant, la plupart des gaz sont en accord approximatif à des pressions et des températures supérieures à leur point d’ébullition. La loi du gaz parfait est utilisée par les ingénieurs travaillant avec les gaz car elle est simple à utiliser et se rapproche du comportement réel du gaz.
La deuxième loi de Joule
Pour tout gaz dont l’équation d’état est donnée exactement par pV = nRT (ou pv = RT ), l’ énergie interne spécifique dépend uniquement de la température. Cette règle a été découverte à l’origine en 1843 par un physicien anglais James Prescott Joule expérimentalement pour les gaz réels et est connue comme le deuxième principe de Joule :
L’énergie interne d’une masse fixe d’un gaz parfait ne dépend que de sa température (et non de la pression ou du volume).
L’ enthalpie spécifique d’un gaz décrite par pV = nRT dépend également uniquement de la température. Notez que l’ enthalpie est la quantité thermodynamique équivalente à la chaleur totale d’un système. Elle est égale à l’énergie interne du système plus le produit de la pression et du volume. Dans les variables intensives, la deuxième loi de Joule est donc donnée par h = h (T) = u (T) + pv = u (T) + RT.
Ces trois équations constituent le modèle de gaz parfait, résumé comme suit:
pv = RT
u = u (T)
h = h (T) = u (T) + RT
Loi du gaz parfait
Toute équation qui relie la pression, la température et le volume spécifique d’une substance est appelée une équation d’état . L’ équation d’état la plus simple et la plus connue pour les substances en phase gazeuse est l’ équation d’état du gaz parfait . Émile Clapeyron l’a déclaré pour la première fois en 1834 comme une combinaison de la loi empirique de Boyle, de la loi de Charles et de la loi d’Avogadro. Cette équation prédit le comportement pvT d’un gaz de façon assez précise pour les gaz dilués ou à basse pression. Dans un gaz parfait, les molécules n’ont pas de volume et n’interagissent pas. Selon la loi du gaz parfait, la pression varie linéairement avec la température et la quantité , et inversement avec le volume .
pV = nRT
où:
- p est la pression absolue du gaz
- n est la quantité de substance
- T est la température absolue
- V est le volume
- R est la constante de gaz idéale ou universelle,égale au produit de la constante de Boltzmann et de la constante d’Avogadro,
Dans cette équation, le symbole R est une constante appelée constante de gaz universelle qui a la même valeur pour tous les gaz, à savoir R = 8,31 J / mol K.
La puissance de la loi du gaz parfait réside dans sa simplicité . Lorsque deux variables thermodynamiques, p, v et T sont données , la troisième peut être facilement trouvée . De nombreuses conditions physiques des gaz calculées par les ingénieurs correspondent à la description ci-dessus. Peut-être l’utilisation la plus courante du comportement des gaz étudiée par les ingénieurs est celle du processus de compression et du processus d’expansion utilisant des approximations de gaz parfaites.
Lois sur le gaz
En général, les lois des gaz sont des premières équations d’état , qui corrèlent les densités de gaz et de liquides aux températures et aux pressions. Les lois sur le gaz ont été complètement développées à la fin du XVIIIe siècle. Ces lois ou déclarations ont précédé la loi du gaz parfait , car individuellement ces lois sont considérées comme des cas particuliers de l’équation du gaz parfait, avec une ou plusieurs des variables maintenues constantes. Puisqu’ils ont été presque complètement remplacés par l’équation du gaz parfait, il n’est pas habituel que les élèves apprennent ces lois en détail. L’ équation du gaz parfait a été énoncée pour la première fois par Émile Clapeyron en 1834 comme une combinaison de ces lois:
Exemple: Loi des gaz parfaits – Compression de gaz à l’intérieur d’un pressuriseur
La pression dans le circuit primaire des REP est maintenue par un pressuriseur , un récipient séparé qui est connecté au circuit primaire (jambe chaude) et partiellement rempli d’eau qui est chauffée à la température de saturation (point d’ébullition) pour la pression souhaitée par une alimentation électrique immergée radiateurs . Pendant le chauffage de l’installation, le pressuriseur peut être rempli d’azote au lieu de vapeur saturée .
Supposons qu’un pressuriseur contienne 12 m 3 d’azote à 20 ° C et 15 bar . La température est portée à 35 ° C et le volume est réduit à 8,5 m 3 . Quelle est la pression finale du gaz à l’intérieur du pressuriseur? Supposons que le gaz soit idéal.
Solution:
Puisque le gaz est idéal, nous pouvons utiliser la loi du gaz parfait pour relier ses paramètres, à la fois dans l’ état initial i et dans l’ état final f . Donc:
p init V init = nRT init
et
p final V final = nRT final
En divisant la deuxième équation par la première équation et en résolvant pour p f on obtient:
p final = p init T final V init / T init V final
Notez que nous ne pouvons pas convertir les unités de volume et de pression en unités SI de base, car elles s’annulent mutuellement. D’un autre côté, nous devons utiliser Kelvins au lieu de degrés Celsius. Donc T init = 293 K et T final = 308 K.
Il s’ensuit que la pression résultante dans l’état final sera:
p final = (15 bar) x (308 K) x (12 m 3 ) / (293 K) x (8,5 m 3 ) = 22 bar
Validité de la loi des gaz parfaits
Puisque le gaz parfait est défini comme celui dans lequel toutes les collisions entre atomes ou molécules sont parfaitement élastiques et où il n’y a pas de forces d’attraction intermoléculaires, il n’existe pas dans la nature de gaz vraiment idéal. En revanche, tous les gaz réels approchent de l’état idéal à basse pression (densité) . A basse pression, les molécules sont suffisamment éloignées pour ne pas interagir les unes avec les autres.
En d’autres termes, la loi des gaz parfaits n’est précise qu’à des pressions relativement basses (par rapport à la pression critique p cr ) et à des températures élevées (par rapport à la température critique T cr ). À ces paramètres, le facteur de compressibilité, Z = pv / RT , est d’ environ 1 . Le facteur de compressibilité est utilisé pour tenir compte de l’écart par rapport à la situation idéale. Ce facteur de correction dépend de la pression et de la température pour chaque gaz considéré.
Énergie interne d’un gaz parfait
L’ énergie interne est le total de toute l’énergie associée au mouvement des atomes ou des molécules dans le système. Les formes microscopiques d’énergie comprennent celles dues à la rotation , aux vibrations , à la traduction et aux interactions entre les molécules d’une substance.
Gaz monoatomique – Énergie interne
Pour un gaz parfait monatomique (tel que l’hélium, le néon ou l’argon), la seule contribution à l’énergie provient de l’énergie cinétique de translation . L’énergie cinétique de translation moyenne d’un seul atome ne dépend que de la température du gaz et est donnée par l’équation:
K moy = 3/2 kT.
L’énergie interne de n moles d’un gaz monatomique idéal (un atome par molécule) est égale à l’énergie cinétique moyenne par molécule multipliée par le nombre total de molécules, N:
E int = 3/2 NkT = 3/2 nRT
où n est le nombre de moles. Chaque direction (x, y et z) contribue (1/2) nRT à l’ énergie interne . C’est là qu’intervient l’idée d’équipartition d’énergie – toute autre contribution à l’énergie doit également contribuer (1/2) nRT . Comme on peut le voir, l’énergie interne d’un gaz parfait ne dépend que de la température et du nombre de moles de gaz.
Molécule diatomique – Énergie interne
Si les molécules de gaz contiennent plus d’un atome, il existe trois directions de translation et l’énergie cinétique de rotation contribue également, mais uniquement pour les rotations autour de deux des trois axes perpendiculaires. Les cinq contributions à l’énergie (cinq degrés de liberté) donnent:
Gaz idéal diatomique:
E int = 5/2 NkT = 5/2 nRT
Ceci n’est qu’une approximation et s’applique aux températures intermédiaires. Aux basses températures, seule l’ énergie cinétique de translation contribue , et à des températures plus élevées, deux contributions supplémentaires (énergie cinétique et potentielle) proviennent des vibrations. L’ énergie interne sera plus grande à une température donnée que pour un gaz monoatomique, mais elle ne restera fonction que de la température pour un gaz parfait.
L’énergie interne des gaz réels dépend également principalement de la température, mais de la même manière que la loi des gaz parfaits , l’énergie interne des gaz réels dépend également quelque peu de la pression et du volume . Tous les gaz réels approchent de l’état idéal à de faibles pressions (densités). A basse pression, les molécules sont suffisamment éloignées pour ne pas interagir les unes avec les autres. L’énergie interne des liquides et des solides est assez compliquée, car elle comprend l’énergie potentielle électrique associée aux forces (ou liaisons chimiques ) entre les atomes et les molécules.
Chaleur spécifique à volume et pression constants
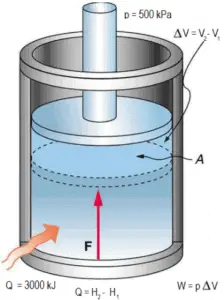
La chaleur spécifique est une propriété liée à l’énergie interne qui est très importante en thermodynamique. Les propriétés intensives c v et c p sont définies pour les substances compressibles pures et simples comme des dérivées partielles de l’ énergie interne u (T, v) et de l’ enthalpie h (T, p) , respectivement:
où les indices v et p désignent les variables maintenues fixes pendant la différenciation. Les propriétés c v et c p sont appelées chaleurs spécifiques (ou capacités calorifiques ) car dans certaines conditions spéciales, elles relient le changement de température d’un système à la quantité d’énergie ajoutée par transfert de chaleur. Les unités SI sont J / kg K ou J / mole K . Deux chaleurs spécifiques sont définies pour les gaz, une pour un volume constant (c v ) et une pour une pression constante (c p ) .
 Selon la première loi de la thermodynamique , pour un procédé à volume constant avec un gaz parfait monatomique, la chaleur spécifique molaire sera:
Selon la première loi de la thermodynamique , pour un procédé à volume constant avec un gaz parfait monatomique, la chaleur spécifique molaire sera:
C v = 3 / 2R = 12,5 J / mol K
car
U = 3 / 2nRT
On peut déduire que la chaleur spécifique molaire à pression constante est:
C p = C v + R = 5 / 2R = 20,8 J / mol K
Ce C p est supérieur à la chaleur spécifique molaire à volume constant C v , car il faut maintenant fournir de l’énergie non seulement pour élever la température du gaz mais aussi pour que le gaz fonctionne car dans ce cas le volume change.
La relation de Mayer – La formule de Mayer
Julius Robert Mayer, chimiste et physicien allemand, a établi une relation entre la chaleur spécifique à pression constante et la chaleur spécifique à volume constant pour un gaz parfait. Il a étudié le fait que la capacité thermique spécifique d’un gaz à pression constante (C p ) est légèrement supérieure à celle à volume constant (C v ). Il a estimé que ce C p est supérieur à la chaleur spécifique molaire à volume constant C v , car l’énergie doit maintenant être fournie non seulement pour élever la température du gaz mais aussi pour que le gaz fonctionne, car dans ce cas, le volume change. Selon leLa relation de Mayer ou la formule de Mayer la différence entre ces deux capacités calorifiques est égale à la constante de gaz universelle, donc la chaleur spécifique molaire à pression constante est égale:
C p = C v + R
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci