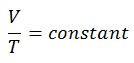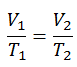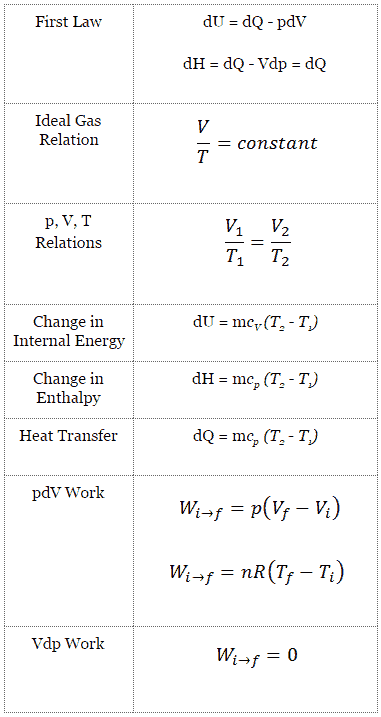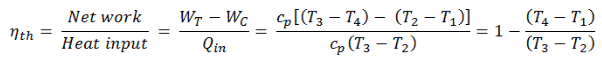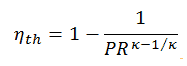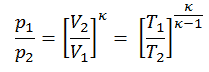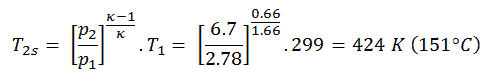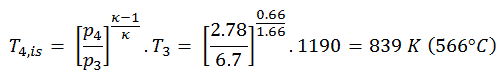Ciclo de Brayton – Turbina a gás
Em 1872, um engenheiro americano, George Bailey Brayton, avançou no estudo de motores térmicos patenteando um motor de combustão interna de pressão constante, inicialmente usando gás vaporizado, mas posteriormente usando combustíveis líquidos, como o querosene. Este mecanismo térmico é conhecido como ” Motor Brayton’s Ready “ . Isso significa que o motor Brayton original usava um compressor de pistão e um expansor de pistão em vez de uma turbina a gás e um compressor de gás.
Hoje, os modernos motores de turbina a gás e os motores a jato de respiração também são motores de calor com pressão constante; portanto, descrevemos sua termodinâmica pelo ciclo de Brayton . Em geral, o ciclo de Brayton descreve o funcionamento de um motor térmico de pressão constante .
É um dos ciclos termodinâmicos mais comuns que podem ser encontrados em usinas de turbinas a gás ou em aviões. Ao contrário do ciclo de Carnot , o ciclo de Brayton não executa processos isotérmicos , porque estes devem ser realizados muito lentamente. Em um ciclo de Brayton ideal , o sistema que executa o ciclo passa por uma série de quatro processos: dois processos isentrópicos (adiabáticos reversíveis) alternados com dois processos isobáricos.
Como o princípio de Carnot afirma que nenhum motor pode ser mais eficiente do que um motor reversível ( um motor térmico de Carnot ) operando entre os mesmos reservatórios de alta temperatura e baixa temperatura, uma turbina a gás baseada no ciclo de Brayton deve ter uma eficiência mais baixa que a eficiência de Carnot.
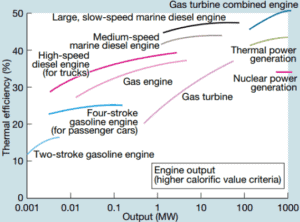
Uma grande turbina a gás de ciclo único normalmente produz, por exemplo, 300 megawatts de energia elétrica e tem 35-40% de eficiência térmica. As modernas instalações de turbinas a gás de ciclo combinado (CCGT), nas quais o ciclo termodinâmico consiste em dois ciclos de usinas (por exemplo, o ciclo de Brayton e o ciclo Rankine), podem atingir uma eficiência térmica de cerca de 55%.
Tipos de turbinas a gás
Em geral, os motores térmicos e também as turbinas a gás são classificados de acordo com um local de combustão como:
- Turbinas com combustão interna . A maioria das turbinas a gás são motores de combustão interna. Nessas turbinas, a alta temperatura é alcançada queimando a mistura combustível-ar na câmara de combustão.
- Turbinas com combustão externa . Nessas turbinas, geralmente é usado um trocador de calor e apenas o meio limpo sem produtos de combustão viaja através da turbina elétrica. Como as pás da turbina não estão sujeitas a produtos de combustão, combustíveis de qualidade muito mais baixa (e, portanto, mais baratos) podem ser usados. Essas turbinas geralmente têm menor eficiência térmica do que as turbinas com combustão interna.
Tipos de Ciclo de Brayton
Ciclo aberto de Brayton (palavras-chave)
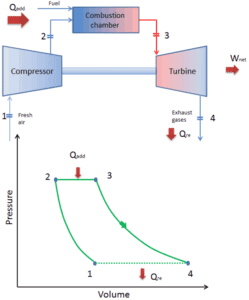
Como a maioria das turbinas a gás é baseada no ciclo de Brayton com combustão interna (por exemplo, motores a jato), elas são baseadas no ciclo aberto de Brayton . Nesse ciclo, o ar da atmosfera ambiente é comprimido para uma pressão e temperatura mais altas pelo compressor. Na câmara de combustão, o ar é aquecido ainda mais pela queima da mistura combustível-ar no fluxo de ar. Os produtos e gases de combustão expandem-se na turbina para perto da pressão atmosférica (motores que produzem energia mecânica ou energia elétrica) ou para uma pressão exigida pelos motores a jato. O ciclo aberto de Brayton significa que os gases são descarregados diretamente na atmosfera .
Ciclo fechado de Brayton
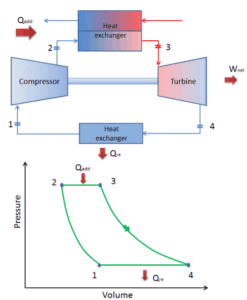
Em um ciclo fechado de Brayton, o meio de trabalho (por exemplo, hélio) recircula no circuito e o gás expelido da turbina é reintroduzido no compressor. Nessas turbinas, geralmente é usado um trocador de calor (combustão externa) e apenas o meio limpo sem produtos de combustão viaja através da turbina elétrica. O ciclo fechado de Brayton é usado, por exemplo, em turbinas a gás de ciclo fechado e reatores refrigerados a gás de alta temperatura.
Ciclo reverso de Brayton – Ciclo de refrigeração de Brayton
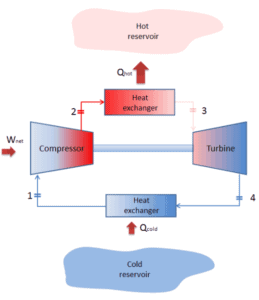
Um ciclo de Brayton conduzido na direção inversa é conhecido como ciclo de Brayton reverso. Seu objetivo é mover o calor do corpo mais frio para o mais quente, em vez de produzir trabalho. De acordo com a segunda lei da termodinâmica, o calor não pode fluir espontaneamente do sistema frio para o sistema quente sem que o trabalho externo seja realizado no sistema. O calor pode fluir do corpo mais frio para o mais quente, mas somente quando forçado por um trabalho externo. É exatamente isso que os refrigeradores e as bombas de calor realizam. Estes são acionados por motores elétricos que exigem trabalho de seu entorno para operar. Um dos ciclos possíveis é o ciclo reverso de Brayton, que é semelhante ao ciclo normal de Brayton, mas é conduzido ao contrário, via entrada líquida de trabalho. Esse ciclo também é conhecido como ciclo de refrigeração a gás ou ciclo de Bell Coleman. Esse tipo de ciclo é amplamente utilizado em aeronaves a jato para sistemas de ar condicionado que utilizam ar dos compressores do motor. Também é amplamente utilizado na indústria de GNL, onde o maior ciclo reverso de Brayton é para sub-resfriamento de GNL usando 86 MW de energia de um compressor acionado por turbina a gás e refrigerante de nitrogênio.
Ciclo de Brayton – Processos
Em um ciclo de Brayton ideal fechado , o sistema que executa o ciclo passa por uma série de quatro processos: dois processos isentrópicos (adiabáticos reversíveis) alternados com dois processos isobáricos:
-
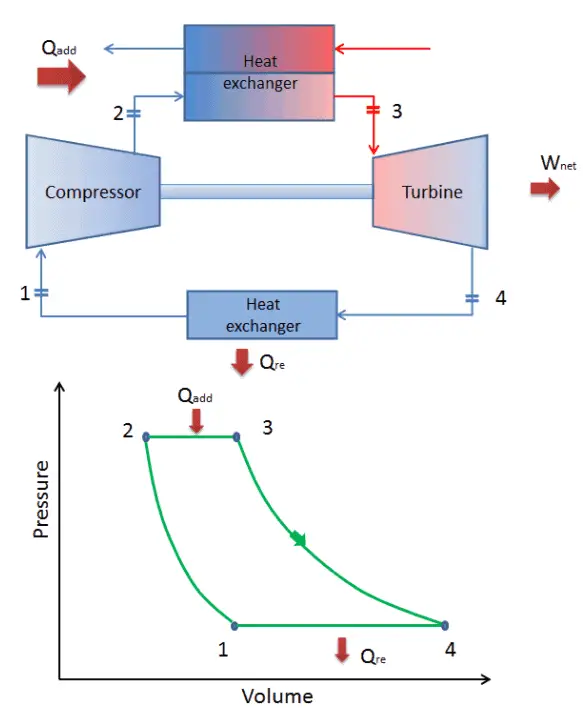
ciclo de Brayton fechado Compressão isentrópica (compressão em um compressor) – O gás de trabalho (por exemplo, hélio) é comprimido adiabaticamente do estado 1 ao estado 2 pelo compressor (geralmente um compressor de fluxo axial). O ambiente trabalha com o gás, aumentando sua energia interna (temperatura) e comprimindo-o (aumentando sua pressão). Por outro lado, a entropia permanece inalterada. O trabalho necessário para o compressor é dado por W C = H 2 – H 1 .
- Adição de calor isobárico (em um trocador de calor) – Nesta fase (entre o estado 2 e o estado 3), há uma transferência de calor de pressão constante para o gás a partir de uma fonte externa, uma vez que a câmara está aberta para entrar e sair. Em um ciclo Brayton ideal aberto, o ar comprimido passa por uma câmara de combustão, onde o combustível é queimado e o ar ou outro meio é aquecido (2 → 3). É um processo de pressão constante, já que a câmara está aberta para entrar e sair. O calor líquido adicionado é dado por Q add = H 3 – H 2
- Expansão isentrópica (expansão em uma turbina) – O gás comprimido e aquecido se expande adiabaticamente do estado 3 para o estado 4 em uma turbina. O gás trabalha nos arredores (pás da turbina) e perde uma quantidade de energia interna igual ao trabalho que sai do sistema. O trabalho realizado pela turbina é dado por W T = H 4 – H 3 . Novamente a entropia permanece inalterada.
- Rejeição de calor isobárica (em um trocador de calor) – Nesta fase, o ciclo é concluído por um processo de pressão constante no qual o calor é rejeitado pelo gás. A temperatura do gás de trabalho cai do ponto 4 para o ponto 1. O calor líquido rejeitado é dado por Q re = H 4 – H 1
Durante um ciclo de Brayton, o trabalho é realizado sobre o gás pelo compressor entre os estados 1 e 2 ( i sentropic compressão ). O trabalho é realizado pelo gás na turbina entre as fases 3 e 4 ( i expansão sentropic ). A diferença entre o trabalho realizado pelo gás e o trabalho realizado no gás é o trabalho líquido produzido pelo ciclo e corresponde à área delimitada pela curva do ciclo (no diagrama pV).
Como pode ser visto, é conveniente usar entalpia ou entalpia específica e expressar a primeira lei em termos de entalpia na análise desse ciclo termodinâmico. Esta forma da lei simplifica a descrição da transferência de energia . A pressão constante , a mudança de entalpia é igual à energia transferida do ambiente através do aquecimento:
Processo isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Na entropia constante , ou seja, no processo isentrópico, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no ou pelo sistema:
Processo isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1
Veja também: Por que os engenheiros de energia usam entalpia? Resposta: dH = dQ + Vdp
Processo isentrópico
Um processo isentrópico é um processo termodinâmico , no qual a entropia do fluido ou gás permanece constante. Isso significa que o processo isentrópico é um caso especial de um processo adiabático no qual não há transferência de calor ou matéria. É um processo adiabático reversível . A suposição de que não há transferência de calor é muito importante, pois podemos usar a aproximação adiabática apenas em processos muito rápidos .
Processo isentrópico e a primeira lei
Para um sistema fechado, podemos escrever a primeira lei da termodinâmica em termos de entalpia :
dH = dQ + Vdp
ou
dH = TdS + Vdp
Processo isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C P (T 2 – T 1 ) (para gás ideal )
Processo isentrópico do gás ideal
O processo isentrópico (um caso especial de processo adiabático) pode ser expresso com a lei dos gases ideais como:
pV κ = constante
ou
p 1 V 1 k = p 2 V 2 k
em que κ = c p / c v é a proporção de aquecimentos específicos (ou capacidades de calor ) para o gás. Um para pressão constante (c p ) e outro para volume constante (c v ) . Observe que essa razão κ = c p / c v é um fator na determinação da velocidade do som em um gás e em outros processos adiabáticos.
Processo isobárico
Um processo isobárico é um processo termodinâmico , no qual a pressão do sistema permanece constante (p = const). A transferência de calor para dentro ou para fora do sistema funciona, mas também altera a energia interna do sistema.
Como existem mudanças na energia interna (dU) e no volume do sistema (∆V), os engenheiros costumam usar a entalpia do sistema, que é definida como:
H = U + pV
Processo isobárico e a primeira lei
A forma clássica da primeira lei da termodinâmica é a seguinte equação:
dU = dQ – dW
Nesta equação, dW é igual a dW = pdV e é conhecido como trabalho de fronteira . Em um processo isobárico e no gás ideal, parte do calor adicionado ao sistema será usada para realizar o trabalho e parte do calor adicionado aumentará a energia interna (aumentará a temperatura). Portanto, é conveniente usar a entalpia em vez da energia interna.
Processo isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Na entropia constante , ou seja, no processo isentrópico, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no sistema ou pelo mesmo.
Processo isobárico do gás ideal
O processo isobárico pode ser expresso com a lei do gás ideal como:
ou
Em um diagrama de pV , o processo ocorre ao longo de uma linha horizontal (chamada isobar) que possui a equação p = constante.
Veja também: Lei de Charles
Ciclo de Brayton – diagrama pV, Ts
O ciclo de Brayton é frequentemente plotado em um diagrama de volume de pressão ( diagrama pV ) e em um diagrama de entropia de temperatura ( diagrama Ts ).
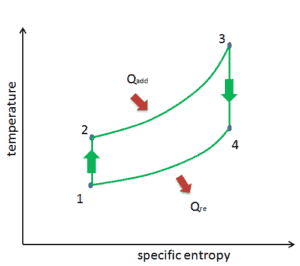
Quando plotados em um diagrama de volume de pressão , os processos isobáricos seguem as linhas isobáricas do gás (as linhas horizontais), os processos adiabáticos se movem entre essas linhas horizontais e a área delimitada pelo caminho completo do ciclo representa o trabalho total que pode ser feito durante um ciclo.
O diagrama de temperatura-entropia ( diagrama Ts) no qual o estado termodinâmico é especificado por um ponto em um gráfico com entropia (s) específica (s) como eixo horizontal e temperatura absoluta (T) como eixo vertical. Os diagramas Ts são uma ferramenta útil e comum, principalmente porque ajuda a visualizar a transferência de calor durante um processo. Para processos reversíveis (ideais), a área sob a curva Ts de um processo é o calor transferido para o sistema durante esse processo.
Eficiência térmica do ciclo de Brayton
Em geral, a eficiência térmica , η th , de qualquer motor de calor é definida como a razão entre o trabalho que faz, W , para o calor de entrada a uma temperatura elevada, Q H .
A eficiência térmica , η th , representa a fração de calor , Q H , que é convertida em trabalho . Como a energia é conservada de acordo com a primeira lei da termodinâmica e a energia não pode ser convertida para funcionar completamente, a entrada de calor, Q H , deve ser igual ao trabalho realizado, W, mais o calor que deve ser dissipado como calor residual Q C no meio Ambiente. Portanto, podemos reescrever a fórmula da eficiência térmica como:
Essa é uma fórmula muito útil, mas aqui expressamos a eficiência térmica usando a primeira lei em termos de entalpia .
Para calcular a eficiência térmica do ciclo de Brayton (compressor único e turbina única), os engenheiros usam a primeira lei da termodinâmica em termos de entalpia e não em energia interna.
A primeira lei em termos de entalpia é:
dH = dQ + Vdp
Nesta equação, o termo Vdp é um trabalho de processo de fluxo. Este trabalho, Vdp , é usado para sistemas de fluxo aberto, como uma turbina ou uma bomba na qual existe um “dp” , ou seja, mudança de pressão. Não há alterações no volume de controle . Como pode ser visto, essa forma de lei simplifica a descrição da transferência de energia .
Existem expressões em termos de variáveis mais familiares, como temperatura e pressão :
dH = C p dT + V (1-aT) dp
Onde C p é a capacidade calorífica a pressão constante e α é o coeficiente de expansão térmica (cúbico). Para o gás ideal αT = 1 e, portanto:
dH = C p dT
A pressão constante , a mudança de entalpia é igual à energia transferida do ambiente através do aquecimento:
Processo isobárico (Vdp = 0):
dH = dQ → Q = H 3 – H 2 → H 3 – H 2 = C P (T 3 – T 2 )
Na entropia constante , ou seja, no processo isentrópico, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no ou pelo sistema:
Processo isentrópico (dQ = 0):
dH = Vdp → W = H 4 – H 3 → H 4 – H 3 = C p (T 4 – T 3 )
A entalpia pode ser transformada em uma variável intensiva ou específica dividindo-se pela massa . Os engenheiros usam mais a entalpia específica na análise termodinâmica do que a própria entalpia.
Agora, vamos assumir o ciclo de Brayton ideal que descreve o funcionamento de um motor de calor com pressão constante. Os modernos motores de turbina a gás e os motores a jato de respiração também seguem o ciclo de Brayton. Esse ciclo consiste em quatro processos termodinâmicos:
-

Ciclo de Brayton – diagrama de Ts compressão isentrópica – o ar ambiente é aspirado para o compressor, onde é pressurizado (1 → 2). O trabalho necessário para o compressor é dado por W C = H 2 – H 1 .
- adição de calor isobárico – o ar comprimido passa por uma câmara de combustão, onde o combustível é queimado e o ar ou outro meio é aquecido (2 → 3). É um processo de pressão constante, já que a câmara está aberta para entrar e sair. O calor líquido adicionado é dado por Q add = H 3 – H 2
- expansão isentrópica – o ar aquecido e pressurizado se expande na turbina, gasta sua energia. O trabalho realizado pela turbina é dado por W T = H 4 – H 3
- rejeição de calor isobárica – o calor residual deve ser rejeitado para fechar o ciclo. O calor líquido rejeitado é dado por Q re = H 4 – H 1
Como pode ser visto, podemos descrever e calcular completamente esses ciclos (da mesma forma para o ciclo de Rankine) usando entalpias.
A eficiência térmica desse ciclo simples de Brayton, para o gás ideal e em termos de entalpias específicas, agora pode ser expressa em termos de temperatura:
Onde
- W t o trabalho realizado pelo gás na turbina
- W C o trabalho realizado no gás no compressor
- c p é a razão de capacidade térmica
Relação de Pressão – Ciclo de Brayton – Turbina a Gás
A eficiência térmica em termos da razão de pressão do compressor (PR = p 2 / p 1 ), que é o parâmetro comumente usado:
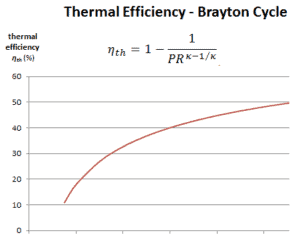 Em geral, aumentar a taxa de pressão é a maneira mais direta de aumentar a eficiência térmica geral de um ciclo de Brayton, porque o ciclo se aproxima do ciclo de Carnot.
Em geral, aumentar a taxa de pressão é a maneira mais direta de aumentar a eficiência térmica geral de um ciclo de Brayton, porque o ciclo se aproxima do ciclo de Carnot.
De acordo com o princípio de Carnot, é possível obter maiores eficiências aumentando a temperatura do gás.
Mas também há limites nas relações de pressão que podem ser usadas no ciclo. A temperatura mais alta do ciclo ocorre no final do processo de combustão e é limitada pela temperatura máxima que as pás da turbina podem suportar. Como de costume, considerações metalúrgicas (cerca de 1700 K) impõem limites superiores à eficiência térmica.
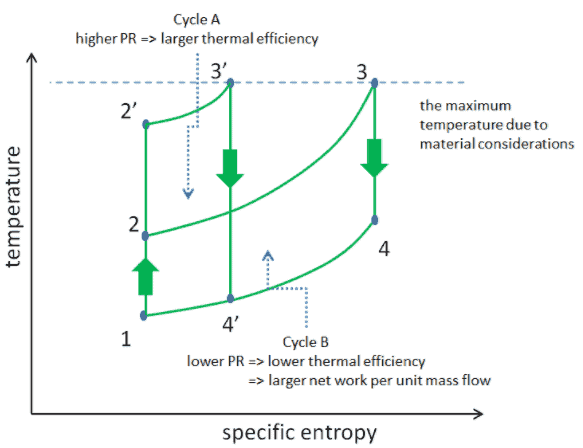
Considere o efeito da taxa de pressão do compressor na eficiência térmica quando a temperatura de entrada da turbina estiver restrita à temperatura máxima permitida. Existem dois diagramas Ts dos ciclos de Brayton com a mesma temperatura de entrada da turbina, mas diferentes proporções de pressão do compressor na imagem. Como pode ser visto para uma temperatura de entrada de turbina fixa, a produção líquida de trabalho por ciclo (W net = W T – W C ) diminui com a razão de pressão ( Ciclo A ). Mas o ciclo A tem a maior eficiência.
Por outro lado, o Ciclo B tem uma maior produção líquida de trabalho por ciclo (área delimitada no diagrama) e, portanto, o maior trabalho líquido desenvolvido por unidade de fluxo de massa. O trabalho produzido pelo ciclo vezes uma taxa de fluxo de massa através do ciclo é igual à potência produzida pela turbina a gás.
Portanto, com menos produção de trabalho por ciclo (Ciclo A), é necessária uma taxa de fluxo de massa maior (portanto, um sistema maior ) para manter a mesma produção de energia, o que pode não ser econômico. Essa é a principal consideração no projeto de turbinas a gás, pois aqui os engenheiros devem equilibrar a eficiência térmica e a compactação. Nos projetos mais comuns, a razão de pressão de uma turbina a gás varia de cerca de 11 a 16.
Melhoria da eficiência térmica – Brayton Cycle
Existem vários métodos, como pode ser melhorada a eficiência térmica do ciclo de Brayton. Assumindo que a temperatura máxima seja limitada por considerações metalúrgicas, esses métodos são:
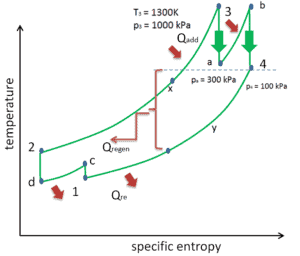
Reaquecimento, Intercooling e Regeneração no Ciclo de Brayton
Como foi discutido, o reaquecimento e o inter-resfriamento são complementares à regeneração de calor . Por si só, eles não necessariamente aumentariam a eficiência térmica; no entanto, quando o inter-resfriamento ou o reaquecimento são usados em conjunto com a regeneração de calor, um aumento significativo na eficiência térmica pode ser alcançado e a produção líquida de trabalho também é aumentada. Isso requer uma turbina a gás com dois estágios de compressão e dois estágios de turbina.
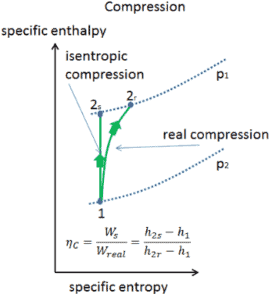
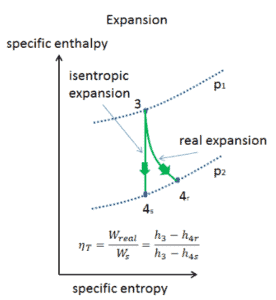
Eficiência isentrópica – turbina, compressor
A maioria dos dispositivos de fluxo constante (turbinas, compressores, bicos) opera em condições adiabáticas , mas não são verdadeiramente isentrópicos, mas são idealizados como isentrópicos para fins de cálculo. Definimos os parâmetros η T , η C , η N , como uma razão entre o trabalho real realizado pelo dispositivo e o trabalho por dispositivo quando operado em condições isentrópicas (no caso de turbinas). Essa relação é conhecida como eficiência isentrópica de turbina / compressor / bico .
Veja também: Irreversibilidade de processos naturais
Esses parâmetros descrevem com que eficiência uma turbina, compressor ou bico se aproxima de um dispositivo isentrópico correspondente. Este parâmetro reduz a eficiência geral e a produção do trabalho. Para turbinas, o valor de η T é tipicamente de 0,7 a 0,9 (70-90%).
Ciclo de Brayton – Problema com a solução
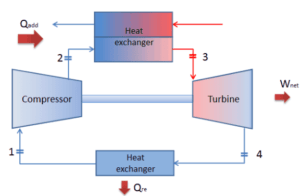 Vamos assumir o ciclo fechado de Brayton , que é um dos ciclos termodinâmicos mais comuns encontrados nos modernos motores de turbina a gás. Nesse caso, assuma uma turbina a gás hélio com um único compressor e arranjo de turbina única. Um dos principais parâmetros de tais motores é a temperatura máxima de entrada da turbina e a taxa de pressão do compressor (PR = p 2 / p 1 ), que determina a eficiência térmica desse motor.
Vamos assumir o ciclo fechado de Brayton , que é um dos ciclos termodinâmicos mais comuns encontrados nos modernos motores de turbina a gás. Nesse caso, assuma uma turbina a gás hélio com um único compressor e arranjo de turbina única. Um dos principais parâmetros de tais motores é a temperatura máxima de entrada da turbina e a taxa de pressão do compressor (PR = p 2 / p 1 ), que determina a eficiência térmica desse motor.
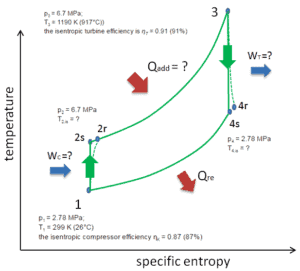
Nesta turbina, o estágio de alta pressão recebe gás (ponto 3 na figura) de um trocador de calor:
- p 3 = 6,7 MPa;
- T 3 = 1190 K (917 ° C))
- a eficiência da turbina isentrópica é η T = 0,91 (91%)
e esvazie-o em outro trocador de calor, onde a pressão de saída é (ponto 4):
- p 4 = 2,78 MPa
- T 4, é =?
Assim, a razão de pressão do compressor é igual a PR = 2,41. Além disso, sabemos que o compressor recebe gás (ponto 1) na figura:
- p 1 = 2,78 MPa;
- T 1 = 299 K (26 ° C)
- a eficiência isentrópica do compressor η K = 0,87 (87%).
A razão de capacidade térmica,, para o hélio é igual a = c p / c v = 1,66
- o calor adicionado pelo trocador de calor (entre 2 → 3)
- a temperatura de saída do compressor do gás (T2 , é )
- o trabalho real realizado neste compressor, quando a eficiência isentrópica do compressor é η K = 0,87 (87%)
- a temperatura de saída da turbina do gás (T 4, é )
- o trabalho real realizado por essa turbina, quando a eficiência da turbina isentrópica é η T = 0,91 (91%)
- a eficiência térmica deste ciclo
Solução:
1) + 2)
A partir da primeira lei da termodinâmica , o calor líquido adicionado é dado por Q add, ex = H 3 – H 2 [kJ] ou Q add = C p . (T 3 -T 2s ) , mas neste caso não sabemos a temperatura (T 2s ) na saída do compressor. Vamos resolver esse problema em variáveis intensivas . Temos que reescrever a equação anterior (para incluir η K ) usando o termo ( + h 1 – h 1 ) para:
Q adicione = h 3 – h 2 = h 3 – h 1 – (h 2 s – h 1 ) / η K [kJ / kg]
Q add = c p (T 3 -T 1 ) – (c p (t 2s -T 1 ) / η K )
Em seguida, iremos calcular a temperatura, T 2s , utilizando p, V, T Relação (a partir de lei do gás ideal ) para processo adiabático entre (1 → 2).
Nesta equação, o fator para o hélio é igual a = c p / c v = 1,66. A partir da equação anterior segue-se que a temperatura de saída do compressor, t 2s , é:
Usando esta temperatura e a eficiência isentrópica do compressor , podemos calcular o calor adicionado pelo trocador de calor:Q add = c p (T 3 -T 1 ) – (c p (t 2s -T 1 ) / η K ) = 5200. (1190 – 299) – 5200. (424-299) /0.87 = 4,633 MJ / kg – 0,747 MJ / kg = 3,886 MJ / kg
3)
O trabalho realizado no gás pelo compressor no processo de compressão isentrópica é:
W C, S = C p (t 2s – T 1 ) = 5200 x (424 – 299) = 0,650 MJ / kg
O trabalho real feito no gás pelo compressor na compressão adiabática é então:
W C, verdadeiro = c p (t 2s – T 1 ). η C = 5200 x (424 – 299) / 0,87 = 0,747 MJ / kg
4)
A temperatura de saída da turbina do gás, T4 , é , pode ser calculada usando a mesma relação p, V, T que em 2), mas entre os estados 3 e 4:
A partir da equação anterior, segue que a temperatura de saída do gás, T 4 , é:
5)
O trabalho realizado pela turbina a gás na expansão isentrópica é então:
W T, s = c p ( T3 – T4s ) = 5200 x (1190 – 839) = 1,825 MJ / kg
O verdadeiro trabalho realizado pela turbina a gás na expansão adiabática é então:
WT , real = cp ( T3 – T4s ). η T = 5200 x (1190 – 839) x 0,91 = 1,661 MJ / kg
6)
Como foi derivado na seção anterior, a eficiência térmica de um ciclo de Brayton ideal é uma função da razão de pressão e κ :
Portanto
η th = 0,295 = 29,5%
A eficiência térmica também pode ser calculada usando o trabalho e o calor (sem η K ):
η th, s = ( WT , s – WC , s ) / adição de Q , s = (1,825 – 0,650) / 3,983 = 0,295 = 29,5%
Finalmente, a eficiência térmica, incluindo a eficiência isentrópica de turbina / compressor, é:
η th, real = ( WT , real – WC , real ) / Q add = (1,661 – 0,747) / 3,886 = 0,235 = 23,5%
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.