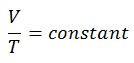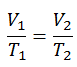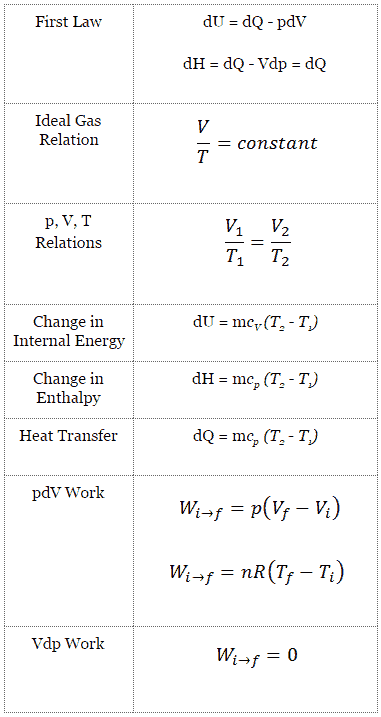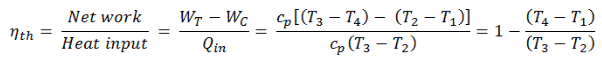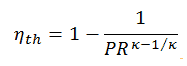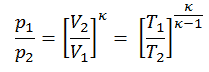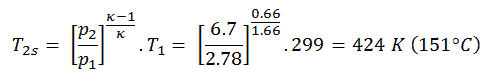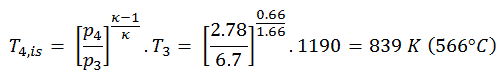Cycle de Brayton – Turbine Engine
En 1872, un ingénieur américain, George Bailey Brayton, a fait progresser l’étude des moteurs thermiques en brevetant un moteur à combustion interne à pression constante, utilisant initialement du gaz vaporisé mais plus tard des combustibles liquides tels que le kérosène. Ce moteur thermique est connu sous le nom de « Moteur prêt de Brayton » . Cela signifie que le moteur Brayton d’origine utilisait un compresseur à piston et un détendeur à piston au lieu d’une turbine à gaz et d’un compresseur à gaz.
Aujourd’hui, les moteurs à turbine à gaz modernes et les moteurs à réaction à respiration aérodynamique sont également des moteurs thermiques à pression constante, c’est pourquoi nous décrivons leur thermodynamique par le cycle de Brayton . En général, le cycle de Brayton décrit le fonctionnement d’un moteur thermique à pression constante .
C’est l’un des cycles thermodynamiques les plus courants que l’on retrouve dans les centrales à turbine à gaz ou dans les avions. Contrairement au cycle de Carnot , le cycle de Brayton n’exécute pas de processus isothermes , car ceux-ci doivent être effectués très lentement. Dans un cycle de Brayton idéal , le système exécutant le cycle subit une série de quatre processus: deux processus isentropiques (adiabatiques réversibles) alternés avec deux processus isobares.
Étant donné que le principe de Carnot stipule qu’aucun moteur ne peut être plus efficace qu’un moteur réversible ( un moteur thermique Carnot ) fonctionnant entre les mêmes réservoirs à haute et à basse température, une turbine à gaz basée sur le cycle de Brayton doit avoir un rendement inférieur à celui de Carnot.
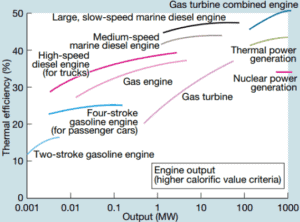
Une grande turbine à gaz à cycle unique produit généralement par exemple 300 mégawatts d’énergie électrique et a une efficacité thermique de 35 à 40%. Les centrales modernes à turbine à gaz à cycle combiné (CCGT), dans lesquelles le cycle thermodynamique se compose de deux cycles de centrale électrique (par exemple le cycle de Brayton et le cycle de Rankine), peuvent atteindre une efficacité thermique d’environ 55%.
Types de turbines à gaz
En général, les moteurs thermiques ainsi que les turbines à gaz sont classés selon un emplacement de combustion comme:
- Turbines à combustion interne . La plupart des turbines à gaz sont des moteurs à combustion interne. Dans ces turbines, la température élevée est atteinte en brûlant le mélange carburant-air dans la chambre de combustion.
- Turbines à combustion externe . Dans ces turbines, un échangeur de chaleur est généralement utilisé et seul un milieu propre sans produits de combustion traverse la turbine de puissance. Comme les aubes de turbine ne sont pas soumises à des produits de combustion, des carburants de bien moindre qualité (et donc moins chers) peuvent être utilisés. Ces turbines ont généralement un rendement thermique inférieur à celui des turbines à combustion interne.
Types de cycle de Brayton
Cycle de Brayton ouvert (mots clés)
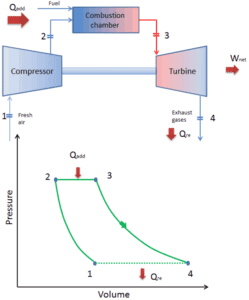
Comme la plupart des turbines à gaz sont basées sur le cycle de Brayton à combustion interne (par exemple les moteurs à réaction), elles sont basées sur le cycle de Brayton ouvert . Dans ce cycle, l’air de l’atmosphère ambiante est comprimé à une pression et une température plus élevées par le compresseur. Dans la chambre de combustion, l’air est davantage chauffé en brûlant le mélange carburant-air dans le flux d’air. Les produits de combustion et les gaz se dilatent dans la turbine soit à une pression proche de la pression atmosphérique (moteurs produisant de l’énergie mécanique ou électrique) soit à une pression requise par les turboréacteurs. Le cycle ouvert de Brayton signifie que les gaz sont rejetés directement dans l’atmosphère .
Cycle de Brayton fermé
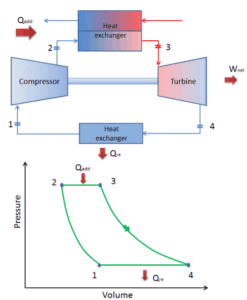
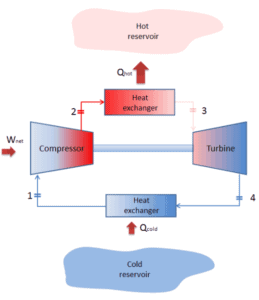
Dans un cycle de Brayton fermé, un milieu de travail (par exemple de l’hélium) recircule dans la boucle et le gaz expulsé de la turbine est réintroduit dans le compresseur. Dans ces turbines, un échangeur de chaleur (combustion externe) est généralement utilisé et seul un fluide propre sans produits de combustion traverse la turbine de puissance. Le cycle fermé de Brayton est utilisé, par exemple, dans les turbines à gaz à cycle fermé et les réacteurs refroidis au gaz à haute température.
Cycle inversé de Brayton – Cycle de réfrigération de Brayton
Un cycle de Brayton entraîné en sens inverse est appelé cycle de Brayton inversé. Son but est de déplacer la chaleur d’un corps plus froid vers un corps plus chaud, plutôt que de produire du travail. Conformément à le deuxième principe de la thermodynamique, la chaleur ne peut pas circuler spontanément du système froid au système chaud sans qu’un travail externe soit effectué sur le système. La chaleur peut circuler d’un corps plus froid vers un corps plus chaud, mais uniquement lorsqu’elle est forcée par un travail extérieur. C’est exactement ce que les réfrigérateurs et les pompes à chaleur accomplissent. Ceux-ci sont entraînés par des moteurs électriques nécessitant un travail de leur environnement pour fonctionner. L’un des cycles possibles est un cycle de Brayton inversé, qui est similaire au cycle Brayton ordinaire mais il est entraîné en sens inverse, via une entrée de travail nette. Ce cycle est également connu sous le nom de cycle de réfrigération au gaz ou cycle de Bell Coleman. Ce type de cycle est largement utilisé dans les avions à réaction pour les systèmes de climatisation utilisant l’air des compresseurs du moteur. Il est également largement utilisé dans l’industrie du GNL où le plus grand cycle inversé de Brayton est pour le sous-refroidissement du GNL en utilisant 86 MW de puissance provenant d’un compresseur entraîné par turbine à gaz et d’un réfrigérant à l’azote.
Cycle de Brayton – Processus
Dans un cycle de Brayton idéal fermé , le système exécutant le cycle subit une série de quatre processus: deux processus isentropiques (adiabatiques réversibles) alternés avec deux processus isobares:
-
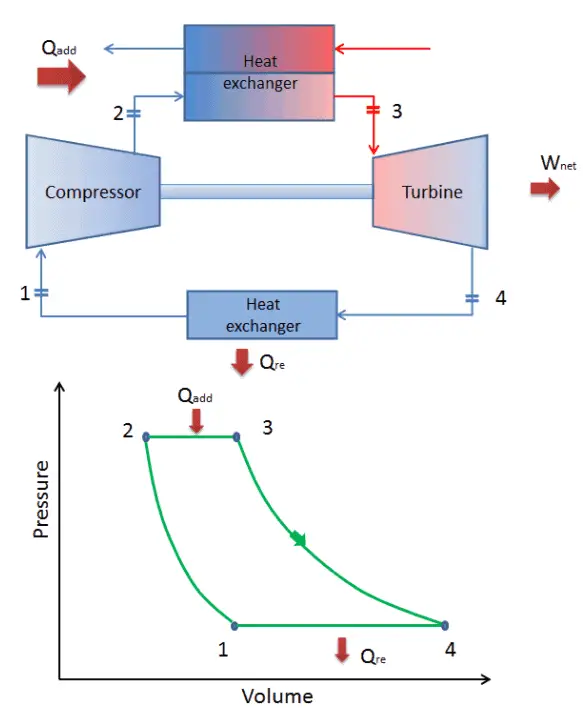
cycle de Brayton fermé Compression isentropique (compression dans un compresseur) – Le gaz de travail (par exemple l’hélium) est comprimé de manière adiabatique de l’état 1 à l’état 2 par le compresseur (généralement un compresseur à flux axial). L’environnement travaille sur le gaz, augmentant son énergie interne (température) et le compressant (augmentant sa pression). En revanche, l’entropie reste inchangée. Le travail requis pour le compresseur est donné par W C = H 2 – H 1 .
- Apport de chaleur isobare (dans un échangeur de chaleur) – Dans cette phase (entre l’état 2 et l’état 3), il y a un transfert de chaleur à pression constante vers le gaz depuis une source externe, car la chambre est ouverte pour entrer et sortir. Dans un cycle de Brayton idéal ouvert, l’air comprimé traverse ensuite une chambre de combustion, où le carburant est brûlé et l’air ou un autre milieu est chauffé (2 → 3). Il s’agit d’un processus à pression constante, car la chambre est ouverte pour entrer et sortir. La chaleur nette ajoutée est donnée par Q add = H 3 – H 2
- Expansion isentropique (expansion dans une turbine) – Le gaz comprimé et chauffé se détend adiabatiquement de l’état 3 à l’état 4 dans une turbine. Le gaz travaille sur l’environnement (pales de la turbine) et perd une quantité d’énergie interne égale au travail qui quitte le système. Le travail effectué par turbine est donné par W T = H 4 – H 3 . Encore une fois, l’entropie reste inchangée.
- Rejet de chaleur isobare (dans un échangeur de chaleur) – Dans cette phase, le cycle se termine par un processus à pression constante dans lequel la chaleur est rejetée du gaz. La température du gaz de travail chute du point 4 au point 1. La chaleur nette rejetée est donnée par Q re = H 4 – H 1
Lors d’un cycle de Brayton, des travaux sont effectués sur le gaz par le compresseur entre les états 1 et 2 ( i compression sentropique ). Le travail est effectué par le gaz dans la turbine entre les étapes 3 et 4 ( i expansion sentropique ). La différence entre le travail effectué par le gaz et le travail effectué sur le gaz est le travail net produit par le cycle et il correspond à l’aire délimitée par la courbe du cycle (en diagramme pV).
Comme on peut le voir, il est commode d’utiliser l’ enthalpie ou l’ enthalpie spécifique et d’exprimer la première loi en termes d’enthalpie dans l’analyse de ce cycle thermodynamique. Cette forme de loi simplifie la description du transfert d’énergie . À pression constante , le changement d’enthalpie est égal à l’ énergie transférée de l’environnement par le chauffage:
Processus isobare (Vdp = 0):
dH = dQ → Q = H 2 – H 1
À entropie constante , c’est-à-dire dans un processus isentropique, le changement d’enthalpie est égal au travail de processus d’écoulement effectué sur ou par le système:
Processus isentropique (dQ = 0):
dH = Vdp → W = H 2 – H 1
Voir aussi: Pourquoi les ingénieurs motoristes utilisent l’enthalpie? Réponse: dH = dQ + Vdp
Processus isentropique
Un processus isentropique est un processus thermodynamique , dans lequel l’ entropie du fluide ou du gaz reste constante. Cela signifie que le processus isentropique est un cas particulier d’un processus adiabatique dans lequel il n’y a pas de transfert de chaleur ou de matière. Il s’agit d’un processus adiabatique réversible . L’hypothèse d’absence de transfert de chaleur est très importante, car nous ne pouvons utiliser l’approximation adiabatique que dans des processus très rapides .
Processus isentropique et première loi
Pour un système fermé, on peut écrire la première loi de la thermodynamique en termes d’enthalpie :
dH = dQ + Vdp
ou
dH = TdS + Vdp
Processus isentropique (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 ) (pour le gaz parfait )
Processus isentropique du gaz parfait
Le processus isentropique (un cas particulier du processus adiabatique) peut être exprimé avec la loi du gaz parfait comme:
pV κ = constant
ou
p 1 V 1 κ = p 2 V 2 κ
dans laquelle κ = c p / c v est le rapport des chaleurs spécifiques (ou capacités calorifiques ) pour le gaz. Un pour une pression constante (c p ) et un pour un volume constant (c v ) . Notez que ce rapport κ = c p / c v est un facteur déterminant la vitesse du son dans un gaz et d’autres processus adiabatiques.
Processus isobare
Un processus isobare est un processus thermodynamique , dans lequel la pression du système reste constante (p = const). Le transfert de chaleur dans ou hors du système fonctionne, mais modifie également l’énergie interne du système.
Puisqu’il y a des changements d’ énergie interne (dU) et des changements de volume du système (∆V), les ingénieurs utilisent souvent l’ enthalpie du système, qui est définie comme:
H = U + pV
Processus isobare et première loi
La forme classique de la première loi de la thermodynamique est l’équation suivante:
dU = dQ – dW
Dans cette équation, dW est égal à dW = pdV et est connu comme le travail aux limites . Dans un procédé isobare et le gaz parfait, une partie de la chaleur ajoutée au système sera utilisée pour faire le travail et une partie de la chaleur ajoutée augmentera l’ énergie interne (augmentera la température). Par conséquent, il est commode d’utiliser l’ enthalpie au lieu de l’énergie interne.
Processus isobare (Vdp = 0):
dH = dQ → Q = H 2 – H 1
À entropie constante , c’est-à-dire dans un processus isentropique, le changement d’enthalpie est égal au travail de processus d’écoulement effectué sur ou par le système.
Processus isobare du gaz parfait
Le processus isobare peut s’exprimer avec la loi du gaz parfait comme:
ou
Sur un diagramme pV , le processus se produit le long d’une ligne horizontale (appelée isobare) qui a l’équation p = constante.
Voir aussi: Charles’s Law
Cycle de Brayton – diagramme pV, Ts
Le cycle de Brayton est souvent tracé sur un diagramme pression-volume (diagramme pV ) et sur un diagramme température-entropie ( diagramme Ts ).
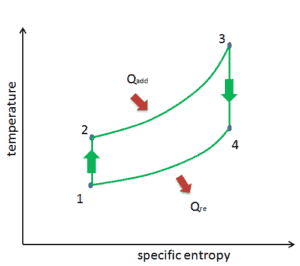
Lorsqu’ils sont tracés sur un diagramme de volume de pression , les processus isobares suivent les lignes isobares pour le gaz (les lignes horizontales), les processus adiabatiques se déplacent entre ces lignes horizontales et la zone délimitée par la piste cyclable complète représente le travail total qui peut être effectué au cours d’une cycle.
Le diagramme température-entropie (diagramme Ts) dans laquelle l’état thermodynamique est défini par un point sur un graphique avec l’ entropie déterminée (s) en tant que l’axe horizontal et la température absolue (T) comme axe vertical. Les diagrammes Ts sont un outil utile et courant, notamment parce qu’il permet de visualiser le transfert de chaleur au cours d’un processus. Pour les processus réversibles (idéaux), l’aire sous la courbe Ts d’un processus est la chaleur transférée au système pendant ce processus.
Efficacité thermique du cycle de Brayton
En général , le rendement thermique , η e , d’un moteur thermique est définie comme étant le rapport entre le travail qu’elle fait, W , à la chaleur d’ entrée à la température élevée, Q H .
L’ efficacité thermique , η th , représente la fraction de chaleur , Q H , qui est convertie en travail . Puisque l’énergie est conservée selon la première loi de la thermodynamique et que l’énergie ne peut pas être convertie pour fonctionner complètement, l’apport de chaleur, Q H , doit être égal au travail effectué, W, plus la chaleur qui doit être dissipée sous forme de chaleur résiduelle Q C dans le environnement. Par conséquent, nous pouvons réécrire la formule de l’efficacité thermique comme suit:
C’est une formule très utile, mais ici nous exprimons l’efficacité thermique en utilisant le première principe en termes d’ enthalpie .
Pour calculer l’efficacité thermique du cycle de Brayton (compresseur unique et turbine unique), les ingénieurs utilisent la première loi de la thermodynamique en termes d’enthalpie plutôt qu’en termes d’énergie interne.
La première loi en matière d’enthalpie est:
dH = dQ + Vdp
Dans cette équation, le terme Vdp est un travail de processus d’écoulement. Ce travail, Vdp , est utilisé pour des systèmes à flux ouvert comme une turbine ou une pompe dans lesquels il y a un «dp» , c’est-à-dire un changement de pression. Il n’y a aucun changement dans le volume de contrôle . Comme on peut le voir, cette forme de loi simplifie la description du transfert d’énergie .
Il existe des expressions en termes de variables plus familières telles que la température et la pression :
dH = C p dT + V (1-αT) dp
Où C p est la capacité thermique à pression constante et α est le coefficient de dilatation thermique (cubique). Pour un gaz parfait αT = 1 et donc:
dH = C p dT
À pression constante , le changement d’enthalpie est égal à l’ énergie transférée de l’environnement par le chauffage:
Processus isobare (Vdp = 0):
dH = dQ → Q = H 3 – H 2 → H 3 – H 2 = C p (T 3 – T 2 )
À entropie constante , c’est-à-dire dans un processus isentropique, le changement d’enthalpie est égal au travail de processus d’écoulement effectué sur ou par le système:
Processus isentropique (dQ = 0):
dH = Vdp → W = H 4 – H 3 → H 4 – H 3 = C p (T 4 – T 3 )
L’ enthalpie peut être transformée en une variable intensive ou spécifique , en la divisant par la masse . Les ingénieurs utilisent l’ enthalpie spécifique dans l’analyse thermodynamique plus que l’enthalpie elle-même.
Supposons maintenant le cycle de Brayton idéal qui décrit le fonctionnement d’un moteur thermique à pression constante. Les moteurs à turbine à gaz modernes et les moteurs à réaction à respiration aérodynamique suivent également le cycle de Brayton. Ce cycle comprend quatre processus thermodynamiques:
-

Cycle de Brayton – Diagramme Ts compression isentropique – l’air ambiant est aspiré dans le compresseur, où il est mis sous pression (1 → 2). Le travail requis pour le compresseur est donné par W C = H 2 – H 1 .
- addition de chaleur isobare – l’air comprimé traverse ensuite une chambre de combustion, où le combustible est brûlé et l’air ou un autre milieu est chauffé (2 → 3). Il s’agit d’un processus à pression constante, car la chambre est ouverte pour entrer et sortir. La chaleur nette ajoutée est donnée par Q add = H 3 – H 2
- expansion isentropique – l’air chauffé sous pression se détend ensuite sur la turbine, cède son énergie. Le travail effectué par turbine est donné par W T = H 4 – H 3
- rejet de chaleur isobare – la chaleur résiduelle doit être rejetée afin de fermer le cycle. La chaleur nette rejetée est donnée par Q re = H 4 – H 1
Comme on peut le voir, nous pouvons décrire et calculer complètement ces cycles (de même pour le cycle de Rankine) en utilisant des enthalpies.
L’efficacité thermique d’un cycle de Brayton aussi simple, pour le gaz parfait et en termes d’enthalpies spécifiques, peut maintenant être exprimée en termes de températures:
où
- W T le travail effectué par le gaz dans la turbine
- W C le travail effectué sur le gaz dans le compresseur
- c p est le rapport de capacité thermique
Rapport de pression – Cycle de Brayton – Turbine à gaz
L’ efficacité thermique en termes de rapport de pression du compresseur (PR = p 2 / p 1 ), qui est le paramètre couramment utilisé:
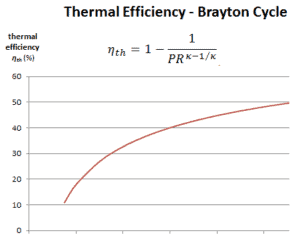 En général, l’ augmentation du rapport de pression est le moyen le plus direct d’augmenter l’efficacité thermique globale d’un cycle de Brayton, car le cycle se rapproche du cycle de Carnot.
En général, l’ augmentation du rapport de pression est le moyen le plus direct d’augmenter l’efficacité thermique globale d’un cycle de Brayton, car le cycle se rapproche du cycle de Carnot.
Selon le principe de Carnot, des rendements plus élevés peuvent être atteints en augmentant la température du gaz.
Mais il y a aussi des limites sur les rapports de pression qui peuvent être utilisés dans le cycle. La température la plus élevée du cycle se produit à la fin du processus de combustion et elle est limitée par la température maximale à laquelle les aubes de turbine peuvent résister. Comme d’habitude, les considérations métallurgiques (environ 1700 K) imposent des limites supérieures à l’efficacité thermique.
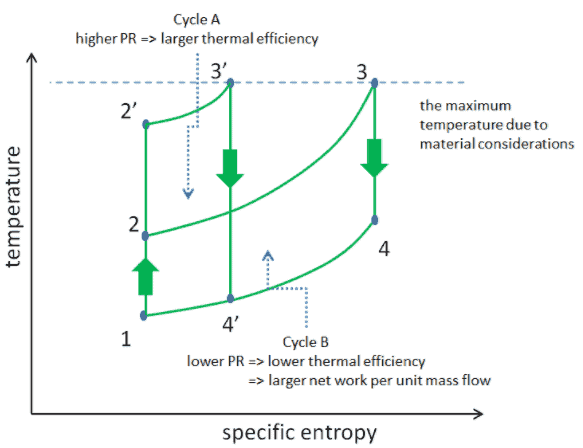
Tenez compte de l’effet du rapport de pression du compresseur sur l’efficacité thermique lorsque la température d’entrée de la turbine est limitée à la température maximale autorisée. Il y a deux diagrammes Ts des cycles de Brayton ayant la même température d’entrée de turbine mais différents rapports de pression de compresseur sur l’image. Comme on peut le voir pour une température d’entrée de turbine fixe, la production nette de travail par cycle (W net = W T – W C ) diminue avec le rapport de pression ( cycle A ). Mais le cycle A a la plus grande efficacité.
D’un autre côté, le cycle B a une production nette de travail plus importante par cycle (zone fermée dans le diagramme) et donc une plus grande production nette développée par unité de débit massique. Le travail produit par le cycle multiplie un débit massique par le cycle est égal à la puissance de sortie produite par la turbine à gaz.
Par conséquent, avec moins de puissance de travail par cycle (cycle A), un débit massique plus important (donc un système plus grand ) est nécessaire pour maintenir la même puissance de sortie, ce qui peut ne pas être économique. C’est la considération clé dans la conception d’une turbine à gaz, car ici les ingénieurs doivent équilibrer l’efficacité thermique et la compacité. Dans la plupart des conceptions courantes, le rapport de pression d’une turbine à gaz varie d’environ 11 à 16.
Amélioration de l’efficacité thermique – cycle de Brayton
Il existe plusieurs méthodes, comment améliorer l’efficacité thermique du cycle de Brayton. En supposant que la température maximale est limitée par des considérations métallurgiques, ces méthodes sont les suivantes:
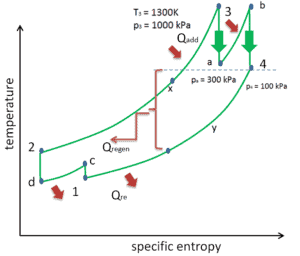
Réchauffage, refroidissement intermédiaire et régénération dans le cycle de Brayton
Comme cela a été discuté, le réchauffage et le refroidissement intermédiaire sont complémentaires de la régénération thermique . En soi, ils n’augmenteraient pas nécessairement l’efficacité thermique.Cependant, lorsque le refroidissement intermédiaire ou le réchauffage est utilisé en conjonction avec la régénération thermique, une augmentation significative de l’efficacité thermique peut être obtenue et la puissance de travail nette est également augmentée. Cela nécessite une turbine à gaz à deux étages de compression et deux étages de turbine.
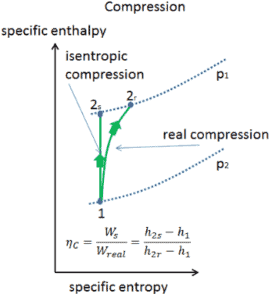
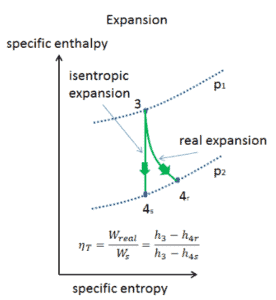
Efficacité isentropique – Turbine, compresseur
La plupart des appareils à débit constant (turbines, compresseurs, buses) fonctionnent dans des conditions adiabatiques , mais ils ne sont pas vraiment isentropiques mais sont plutôt idéalisés comme isentropiques à des fins de calcul. Nous définissons les paramètres η T , η C , η N , comme un rapport entre le travail réel effectué par appareil et le travail par appareil lorsqu’il est utilisé dans des conditions isentropiques (dans le cas d’une turbine). Ce rapport est connu sous le nom d’ efficacité turbine isentropique / compresseur / buse .
Voir aussi: Irréversibilité des processus naturels
Ces paramètres décrivent l’efficacité avec laquelle une turbine, un compresseur ou une buse se rapproche d’un dispositif isentropique correspondant. Ce paramètre réduit l’efficacité globale et le rendement de travail. Pour les turbines, la valeur de η T est généralement de 0,7 à 0,9 (70–90%).
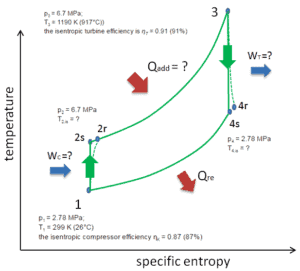
Cycle de Brayton – Problème avec la solution
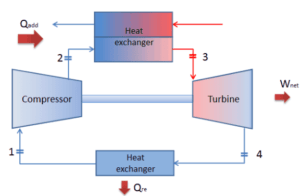 Supposons le cycle de Brayton fermé , qui est l’un des cycles thermodynamiques les plus courants que l’on puisse trouver dans les moteurs à turbine à gaz modernes. Dans ce cas, supposons une turbine à gaz à l’hélium avec un compresseur unique et une seule turbine. L’un des paramètres clés de ces moteurs est la température maximale d’entrée de la turbine et le rapport de pression du compresseur (PR = p 2 / p 1 ) qui détermine l’efficacité thermique de ce moteur.
Supposons le cycle de Brayton fermé , qui est l’un des cycles thermodynamiques les plus courants que l’on puisse trouver dans les moteurs à turbine à gaz modernes. Dans ce cas, supposons une turbine à gaz à l’hélium avec un compresseur unique et une seule turbine. L’un des paramètres clés de ces moteurs est la température maximale d’entrée de la turbine et le rapport de pression du compresseur (PR = p 2 / p 1 ) qui détermine l’efficacité thermique de ce moteur.
Dans cette turbine, l’étage haute pression reçoit du gaz (point 3 sur la figure) d’un échangeur de chaleur:
- p 3 = 6,7 MPa;
- T 3 = 1190 K (917 ° C))
- le rendement de la turbine isentropique est η T = 0,91 (91%)
et l’évacuer vers un autre échangeur de chaleur, où la pression de sortie est (point 4):
- p 4 = 2,78 MPa
- T 4, est =?
Ainsi, le rapport de pression du compresseur est égal à PR = 2,41. De plus on sait, que le compresseur reçoit du gaz (point 1) sur la figure:
- p 1 = 2,78 MPa;
- T 1 = 299 K (26 ° C)
- l’efficacité du compresseur isentropique η K = 0,87 (87%).
Le rapport de capacité thermique,, pour l’hélium est égal à = c p / c v = 1,66
- la chaleur ajoutée par l’échangeur de chaleur (entre 2 → 3)
- la température de sortie du compresseur du gaz (T 2, est )
- le vrai travail effectué sur ce compresseur, lorsque l’efficacité du compresseur isentropique est η K = 0,87 (87%)
- la température de sortie de la turbine du gaz (T 4, est )
- le travail réel effectué par cette turbine, lorsque le rendement de la turbine isentropique est η T = 0,91 (91%)
- l’efficacité thermique de ce cycle
Solution:
1) + 2)
D’après la première loi de la thermodynamique , la chaleur nette ajoutée est donnée par Q add, ex = H 3 – H 2 [kJ] ou Q add = C p . (T 3 -T 2s ) , mais dans ce cas nous ne savons pas la température (T 2s ) à la sortie du compresseur. Nous allons résoudre ce problème en variables intensives . Nous devons réécrire l’équation précédente (pour inclure η K ) en utilisant le terme ( + h 1 – h 1 ) pour:
Q add = h 3 – h 2 = h 3 – h 1 – (h 2s – h 1 ) / η K [kJ / kg]
Q add = c p (T 3 -T 1 ) – (c p (T 2s -T 1 ) / η K )
Ensuite, nous calculerons la température, T 2s , en utilisant la relation p, V, T (de la loi des gaz parfaits ) pour le processus adiabatique entre (1 → 2).
Dans cette équation, le facteur pour l’hélium est égal à = c p / c v = 1,66. D’après l’équation précédente, la température de sortie du compresseur, T 2s , est:
3)
Le travail effectué sur le gaz par le compresseur dans le processus de compression isentropique est:
W C, s = c p (T 2s – T 1 ) = 5200 x (424 – 299) = 0,650 MJ / kg
Le vrai travail effectué sur le gaz par le compresseur dans la compression adiabatique est alors:
W C, réel = c p (T 2s – T 1 ). η C = 5200 x (424 – 299) / 0,87 = 0,747 MJ / kg
4)
La température de sortie de turbine du gaz, T 4, est , peut être calculée en utilisant la même relation p, V, T qu’en 2) mais entre les états 3 et 4:
De l’équation précédente, la température de sortie du gaz, T 4 , est:
5)
Le travail effectué par la turbine à gaz dans l’expansion isentropique est alors:
W T, s = c p (T 3 – T 4s ) = 5200 x (1190 – 839) = 1,825 MJ / kg
Le véritable travail effectué par la turbine à gaz dans l’expansion adiabatique est alors:
W T, réel = c p (T 3 – T 4s ). η T = 5200 x (1190 – 839) x 0,91 = 1,661 MJ / kg
6)
Comme il a été dérivé dans la section précédente, l’ efficacité thermique d’un cycle de Brayton idéal est fonction du rapport de pression et de κ :
par conséquent
η th = 0,295 = 29,5%
L’efficacité thermique peut également être calculée en utilisant le travail et la chaleur (sans η K ):
η th, s = ( W T, s – W C, s ) / Q add, s = (1,825 – 0,650) / 3,998 = 0,295 = 29,5%
Enfin, l’efficacité thermique, y compris l’efficacité turbine / compresseur isentropique, est:
η e, réel = ( W T, réel – W C, réel ) / Q add = (1,661 – 0,747) / 3,886 = 0,235 = 23,5%
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci