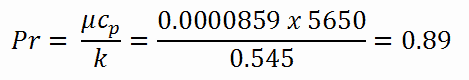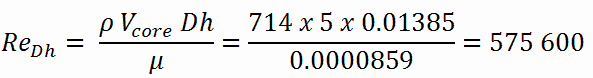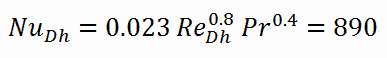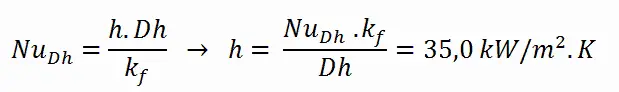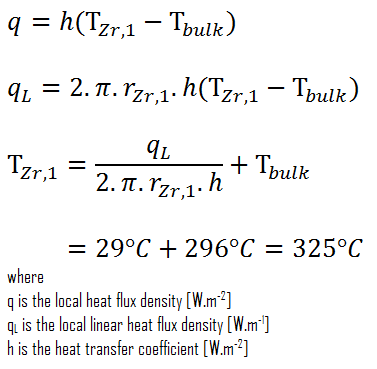O que é a Equação de Dittus-Boelter – Definição

O fator de atrito de Darcy , f,  é uma quantidade adimensional usada na equação de Darcy-Weisbach , para a descrição de perdas por atrito em tubulação ou duto, bem como para fluxo em canal aberto. Isso também é chamado de  fator de atrito de Darcy-Weisbach ,  coeficiente de resistência ou simplesmente  fator de atrito .

Tubos de parede áspera

Também observamos que todas essas equações pertencem a tubos lisos. Para fluxo turbulento em tubos rugosos, o coeficiente de transferência de calor aumenta com a rugosidade da parede . À medida que o número de Reynolds aumenta, a subcamada viscosa se torna mais fina e menor. No número Reynolds muito alto, a subcamada viscosa se torna tão fina que a rugosidade da superfície se projeta no fluxo. As perdas por atrito neste caso são produzidas no fluxo principal principalmente pelos elementos de rugosidade salientes, e a contribuição da subcamada laminar é insignificante.

Referência Especial: Um Livro de Transferência de Calor, John H. Lienhard IV e John H. Lienhard V. Phlogiston Press, 2012.

Exemplo – Equação de Dittus-Boelter – Temperatura da superfície do revestimento

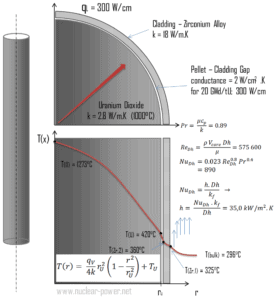O revestimento é a camada externa das barras de combustível, situada entre o líquido de arrefecimento do reator e o combustível nuclear (isto é, granulados de combustível ). É feito de um material resistente à corrosão com seção transversal de baixa absorção para nêutrons térmicos , geralmente liga de zircônio . O revestimento evita que produtos de fissão radioativa escapem da matriz de combustível para o líquido de arrefecimento do reator e os contaminem. O revestimento constitui uma das barreiras na abordagem de ‘ defesa em profundidade ‘; portanto, sua capacidade de refrigeração é um dos principais aspectos de segurança.

Considere o revestimento de combustível do raio interno r _{Zr, 2} = 0,408 cm e raio externo r _{Zr, 1} = 0,465 cm . Em comparação com o pellet de combustível, quase não há geração de calor no revestimento de combustível (o revestimento é levemente aquecido pela radiação ). Todo o calor gerado no combustível deve ser transferido por condução através do revestimento e, portanto, a superfície interna é mais quente que a superfície externa.

Assuma isso:

• o diâmetro externo do revestimento é: d = 2 xr _{Zr, 1} = 9,3 mm
• o passo dos pinos de combustível é: p = 13 mm
• a condutividade térmica da água saturada a 300 ° C é: k _H2O = 0,545 W / mK
• a viscosidade dinâmica da água saturada a 300 ° C é: μ = 0,0000859 Ns / m ²
• a densidade do fluido é: ρ = 714 kg / m ³
• o calor específico é: c _p = 5,65 kJ / kg.K
• a velocidade de fluxo do núcleo é constante e igual a V _core = 5 m / s
• a temperatura do líquido de arrefecimento do reator nesta coordenada axial é: T a _granel = 296 ° C
• a taxa linear de calor do combustível é q _L = 300 W / cm (F _Q ≈ 2.0) e, portanto, a taxa volumétrica de calor é q _V = 597 x 10 ⁶ W / m ³

Calcule o número de Prandtl , Reynolds e Nusselt para esse regime de fluxo (fluxo turbulento forçado interno) dentro da estrutura retangular de combustível (canal de combustível), depois calcule o coeficiente de transferência de calor e, finalmente, a temperatura da superfície do revestimento , T _{Zr, 1} .

Para calcular a temperatura da superfície do revestimento , precisamos calcular o número de Prandtl , Reynolds e Nusselt , porque a transferência de calor para esse regime de fluxo pode ser descrita pela equação de Dittus-Boelter , que é:

Cálculo do número Prandtl

Para calcular o número Prandtl , precisamos saber:

• a condutividade térmica da água saturada a 300 ° C é: k _H2O = 0,545 W / mK
• a viscosidade dinâmica da água saturada a 300 ° C é: μ = 0,0000859 Ns / m ²
• o calor específico é: c _p = 5,65 kJ / kg.K

Observe que todos esses parâmetros diferem significativamente para a água a 300 ° C daqueles a 20 ° C. O número de prandtl para água a 20 ° C é de cerca de 6,91. O número de Prandtl para o líquido de refrigeração do reator a 300 ° C é então:

Cálculo do número de Reynolds

Para calcular o número de Reynolds, precisamos saber:

• o diâmetro externo do revestimento é: d = 2 xr _{Zr, 1} = 9,3 mm (para calcular o diâmetro hidráulico)
• o passo dos pinos de combustível é: p = 13 mm  (para calcular o diâmetro hidráulico)
• a viscosidade dinâmica da água saturada a 300 ° C é: μ = 0,0000859 Ns / m ²
• a densidade do fluido é: ρ = 714 kg / m ³

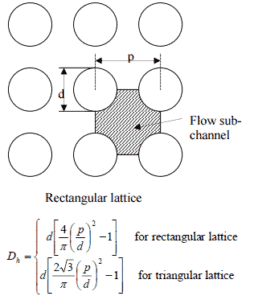
O diâmetro hidráulico, D _h , é um termo comumente usado ao manipular o fluxo em tubos e canais não circulares . O diâmetro hidráulico do canal de combustível , D _h , é igual a 13,85 mm.

Veja também: Diâmetro hidráulico

O número de Reynolds dentro do canal de combustível é então igual a:

Isso satisfaz plenamente as condições turbulentas .

Cálculo do número de Nusselt usando a equação de Dittus-Boelter

Para um fluxo turbulento totalmente desenvolvido (hidrodinamicamente e termicamente) em um tubo circular liso, o número local de Nusselt pode ser obtido a partir da conhecida equação Dittus® Boelter .

Para calcular o número de Nusselt , precisamos saber:

• o número de Reynolds , que é Re _Dh = 575600
• o número Prandtl , que é Pr = 0,89

O número de Nusselt para a convecção forçada dentro do canal de combustível é então igual a:

Cálculo do coeficiente de transferência de calor e da temperatura da superfície do revestimento, T _{Zr, 1}

O conhecimento detalhado da geometria, parâmetros do fluido, raio externo do revestimento, taxa de calor linear, coeficiente de transferência de calor por convecção nos permite calcular a diferença de temperatura ∆T entre o líquido de arrefecimento (T a _granel ) e a superfície do revestimento (T _{Zr, 1} ).

Para calcular a temperatura da superfície do revestimento, precisamos saber:

• o diâmetro externo do revestimento é: d = 2 x r _{Zr, 1} = 9,3 mm
• o número de Nusselt, que é Nu _Dh = 890
• o diâmetro hidráulico do canal de combustível é: D _h = 13,85 mm
• a condutividade térmica do líquido de refrigeração do reator (300 ° C) é: k _H2O = 0,545 W / mK
• a temperatura a granel do líquido de refrigeração do reator nesta coordenada axial é: T a _granel = 296 ° C
• a taxa linear de calor do combustível é: q _L = 300 W / cm (F _Q ≈ 2.0)

O coeficiente de transferência de calor convectivo, h , é dado diretamente pela definição do número de Nusselt:

Finalmente, podemos calcular a temperatura da superfície do revestimento (T _{Zr, 1} ) simplesmente usando a Lei de Newton de resfriamento :

Para PWRs em operação normal, há água líquida comprimida dentro do núcleo do reator, loops e geradores de vapor. A pressão é mantida em aproximadamente 16MPa . A essa pressão, a água ferve a aproximadamente 350 ° C (662 ° F). Como pode ser visto, a temperatura da superfície T _{Zr, 1} = 325 ° C garante que mesmo a ebulição sub-resfriada não ocorra. Observe que a ebulição sub-resfriada requer T _{Zr, 1} = T _sat . Como as temperaturas de entrada da água são geralmente de cerca de 290 ° C(554 ° F), é óbvio que este exemplo corresponde à parte inferior do núcleo. Em elevações mais altas do núcleo, a temperatura a granel pode atingir até 330 ° C. A diferença de temperatura de 29 ° C causa a fervura sub-resfriada (330 ° C + 29 ° C> 350 ° C). Por outro lado, a ebulição nucleada na superfície interrompe efetivamente a camada estagnada e, portanto, a ebulição nucleada aumenta significativamente a capacidade de uma superfície de transferir energia térmica para o fluido a granel. Como resultado, o coeficiente de transferência de calor por convecção aumenta significativamente e, portanto, em elevações mais altas, a diferença de temperatura (T _{Zr, volume 1} – T ) diminui significativamente.