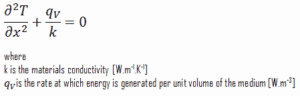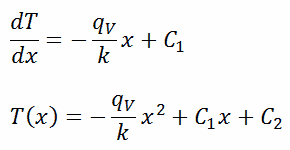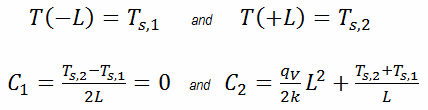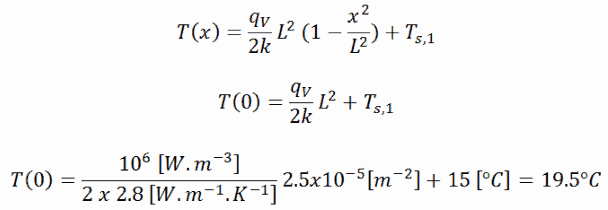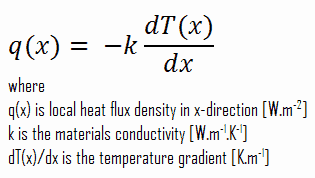Facebook Instagram Youtube Twitter

What is Heat Conduction in a Large Plane Wall – Definition

by
Heat Conduction in a Large Plane Wall. Consider the plane wall of thickness 2L, in which there is uniform and constant heat generation per unit volume, qV [W/m3]. Thermal Engineering

Heat Conduction in a Large Plane Wall

Heat Conduction in a Large Plane Wall

Consider the plane wall of thickness 2L, in which there is uniform and constant heat generation per unit volume, qV [W/m3]. The centre plane is taken as the origin for x and the slab extends to + L on the right and – L on the left. For constant thermal conductivity k, the appropriate form of the heat equation, is:

heat equation - heat generation - equation

The general solution of this equation is:

heat conduction equation - general solution

where C1 and C2 are the constants of integration.

1)

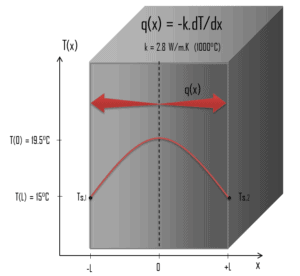Heat Conduction in a Large Plane WallCalculate the temperature distribution, T(x), through this thick plane wall, if:

  • the temperatures at both surfaces are 15.0°C
  • the thickness this wall is 2L = 10 mm.
  • the materials conductivity is k = 2.8 W/m.K (corresponds to uranium dioxide at 1000°C)
  • the volumetric heat rate is qV = 106 W/m3

In this case, the surfaces are maintained at given temperatures Ts,1 and Ts,2. This corresponds to the Dirichlet boundary condition. Moreover, this problem is thermally symmetric and therefore we may use also thermal symmetry boundary condition. The constants may be evaluated using substitution into the general solution and are of the form:

heat conduction equation - boundary conditions

The resulting temperature distribution and the centerline (x = 0) temperature (maximum) in this plane wall at these specific boundary conditions will be:

heat conduction equation - solution

The heat flux at any point, qx [W.m-2], in the wall may, of course, be determined by using the temperature distribution and with the Fourier’s law. Note that, with heat generation the heat flux is no longer independent of x, the therefore:

heat condution through wall

Example of Heat Equation – Problem with Solution

 
References:
Heat Transfer:
  1. Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
  2. Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
  3. Fundamentals of Heat and Mass Transfer. C. P. Kothandaraman. New Age International, 2006, ISBN: 9788122417722.
  4. U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.

Nuclear and Reactor Physics:

  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Heat Equation

We hope, this article, Heat Conduction in a Large Plane Wall, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts