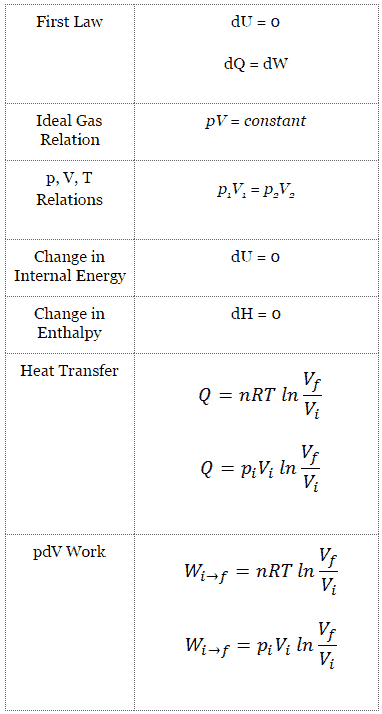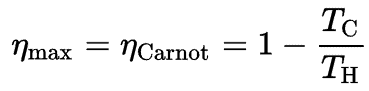Carnot Cycle – Carnot Heat Engine
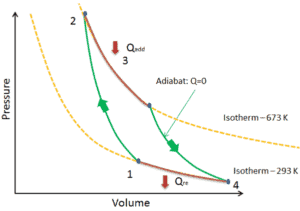
La segunda ley de la termodinámica impone restricciones sobre la dirección de la transferencia de calor y establece un límite superior para la eficiencia de la conversión de calor para trabajar en motores de calor . Entonces, la segunda ley es directamente relevante para muchos problemas prácticos importantes.
En 1824, un ingeniero y físico francés, Nicolas Léonard Sadi Carnot avanzó el estudio de la segunda ley al formar un principio (también llamado la regla de Carnot ) que especifica los límites de la máxima eficiencia que cualquier motor térmico puede obtener. En resumen, este principio establece que la eficiencia de un ciclo termodinámico depende únicamente de la diferencia entre los depósitos de temperatura caliente y fría.
El principio de Carnot establece:
- Ningún motor puede ser más eficiente que un motor reversible ( un motor térmico de Carnot ) que opera entre los mismos depósitos de alta temperatura y baja temperatura.
- Las eficiencias de todos los motores reversibles (motores de calor Carnot ) que funcionan entre los mismos depósitos de temperatura constante son los mismos, independientemente de la sustancia de trabajo empleada o los detalles de operación.
El ciclo de este motor se llama ciclo de Carnot . Un sistema que experimenta un ciclo de Carnot se llama motor de calor de Carnot . No es un ciclo termodinámico real, pero es una construcción teórica y no se puede construir en la práctica. Todos los procesos termodinámicos reales son de alguna manera irreversibles . No se realizan de manera infinitamente lenta e infinitamente pequeños pasos de temperatura también son una ficción teórica. Por lo tanto, los motores térmicos deben tener eficiencias más bajas que los límites en su eficiencia debido a la irreversibilidad inherente del ciclo del motor térmico que usan.
Ciclo de Carnot – Procesos
En un ciclo de Carnot , el sistema que ejecuta el ciclo experimenta una serie de cuatro procesos internamente reversibles : dos procesos isentrópicos (adiabáticos reversibles) alternados con dos procesos isotérmicos :
- compresión isoentrópica – El gas se comprime adiabáticamente del estado 1 al estado 2, donde la temperatura es T H . Los alrededores trabajan con el gas, aumentando su energía interna y comprimiéndolo. Por otro lado, la entropía permanece sin cambios .
- Isotérmica expansión – El sistema se coloca en contacto con el depósito en T H . El gas se expande isotérmicamente mientras recibe energía Q H del depósito caliente por transferencia de calor. La temperatura del gas no cambia durante el proceso. El gas funciona en los alrededores. El cambio total de entropía viene dado por: ∆S = S 1 – S 4 = Q H / T H
- expansión isoentrópica – El gas se expande adiabáticamente del estado 3 al estado 4, donde la temperatura es T C . El gas funciona en el entorno y pierde una cantidad de energía interna igual al trabajo que abandona el sistema. Nuevamente, la entropía permanece sin cambios.
- isotérmica de compresión – El sistema se coloca en contacto con el depósito en T C . El gas se comprime isotérmicamente a su estado inicial mientras descarga energía Q C al depósito frío por transferencia de calor. En este proceso, los alrededores trabajan con el gas. El cambio total de entropía viene dado por: ∆S = S 3 – S 2 = Q C / T C
Proceso isentrópico
Un proceso isentrópico es un proceso termodinámico , en el cual la entropía del fluido o gas permanece constante. Significa que el proceso isentrópico es un caso especial de un proceso adiabático en el que no hay transferencia de calor o materia. Es un proceso adiabático reversible . La suposición de que no hay transferencia de calor es muy importante, ya que podemos usar la aproximación adiabática solo en procesos muy rápidos .
Proceso isentrópico y la primera ley
Para un sistema cerrado, podemos escribir la primera ley de la termodinámica en términos de entalpía :
dH = dQ + Vdp
o
dH = TdS + Vdp
Proceso isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 ) (para gas ideal )
Proceso isentrópico del gas ideal
El proceso isentrópico (un caso especial de proceso adiabático) se puede expresar con la ley de los gases ideales como:
pV κ = constante
o
p 1 V 1 κ = p 2 V 2 κ
en el que κ = c p / c v es la relación de los calores específicos (o capacidades de calor ) para el gas. Uno para presión constante (c p ) y otro para volumen constante (c v ) . Tenga en cuenta que esta relación κ = c p / c v es un factor para determinar la velocidad del sonido en un gas y otros procesos adiabáticos.
Proceso isotérmico
Un proceso isotérmico es un proceso termodinámico , en el que la temperatura del sistema permanece constante (T = constante). La transferencia de calor dentro o fuera del sistema generalmente debe ocurrir a una velocidad tan lenta para ajustarse continuamente a la temperatura del depósito a través del intercambio de calor. En cada uno de estos estados se mantiene el equilibrio térmico .
Proceso isotérmico y la primera ley
La forma clásica de la primera ley de la termodinámica es la siguiente ecuación:
dU = dQ – dW
En esta ecuación, dW es igual a dW = pdV y se conoce como el trabajo límite .
En el proceso isotérmico y el gas ideal , todo el calor agregado al sistema se utilizará para hacer el trabajo:
Proceso isotérmico (dU = 0):
dU = 0 = Q – W → W = Q (para gas ideal)
Proceso isotérmico del gas ideal
El proceso isotérmico se puede expresar con la ley de los gases ideales como:
pV = constante
o
p 1 V 1 = p 2 V 2
En un diagrama de pV, el proceso se produce a lo largo de una línea (llamada una isoterma) que tiene la ecuación p = constante / V .
Ver también: Ley de Boyle-Mariotte
Ciclo de Carnot – pV, diagrama Ts
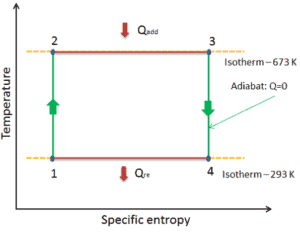
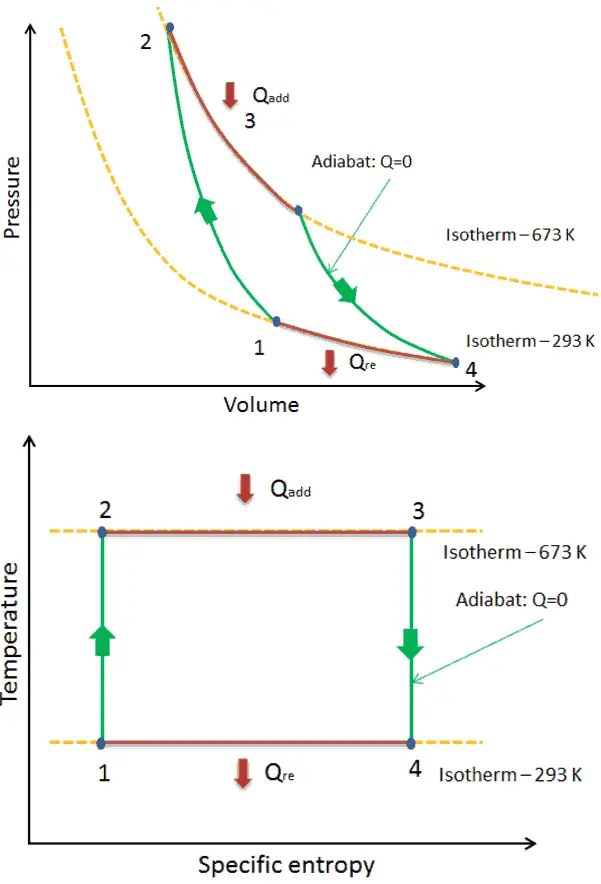
El ciclo de Carnot a menudo se representa en un diagrama de presión-volumen ( diagrama pV ) y en un diagrama de temperatura-entropía ( diagrama Ts ).
Cuando se trazan en un diagrama de presión-volumen , los procesos isotérmicos siguen las líneas isotérmicas del gas, los procesos adiabáticos se mueven entre isotermas y el área delimitada por la ruta completa del ciclo representa el trabajo total que se puede hacer durante un ciclo.
El diagrama de temperatura-entropía ( diagrama Ts) en el que el estado termodinámico se especifica mediante un punto en un gráfico con entropía específica (s) como eje horizontal y temperatura absoluta (T) como eje vertical, es el mejor diagrama para describir el comportamiento de un ciclo de Carnot .
Es una herramienta útil y común, particularmente porque ayuda a visualizar la transferencia de calor durante un proceso. Para procesos reversibles (ideales), el área bajo la curva Ts de un proceso es el calor transferido al sistema durante ese proceso.
Eficiencia del ciclo de Carnot
En general, la eficiencia térmica , η º , de cualquier motor de calor se define como la relación de la red de trabajo que hace, W , para el calor de entrada a la alta temperatura, Q H .
Dado que la energía se conserva de acuerdo con la primera ley de la termodinámica y la energía no se puede convertir en trabajo por completo, la entrada de calor, Q H , debe ser igual al trabajo realizado, W, más el calor que se debe disipar como calor residual Q C en el ambiente. Por lo tanto, podemos reescribir la fórmula para la eficiencia térmica como:
Dado que Q C = ∆ST C y Q H = ∆ST H , la fórmula para esta eficiencia máxima es:
dónde:
- es la eficiencia del ciclo de Carnot, es decir, es la relación = W / Q H del trabajo realizado por el motor a la energía térmica que ingresa al sistema desde el depósito caliente.
- T C es la temperatura absoluta (Kelvins) del depósito frío,
- T H es la temperatura absoluta (Kelvins) del depósito caliente.
Ver también: causas de ineficiencias
Ejemplo: eficiencia de Carnot para una central eléctrica de carbón
En una moderna planta de energía de carbón , la temperatura del vapor de alta presión (T caliente ) sería de unos 400 ° C (673K) y T frío , la temperatura de agua de la torre de refrigeración, sería de alrededor de 20 ° C (293 K). Para este tipo de planta de energía, la eficiencia máxima (ideal) será:
η th = 1 – T frío / T caliente = 1 – 293/673 = 56%
Debe agregarse, esta es una eficiencia idealizada . La eficiencia de Carnot es válida para procesos reversibles. Estos procesos no pueden lograrse en ciclos reales de centrales eléctricas. La eficiencia de Carnot dicta que se pueden lograr mayores eficiencias aumentando la temperatura del vapor. Esta característica es válida también para ciclos termodinámicos reales. Pero esto requiere un aumento de las presiones dentro de las calderas o generadores de vapor . Sin embargo, las consideraciones metalúrgicas ponen límites superiores a tales presiones. Las plantas de energía de combustible fósil subcrítico, que funcionan bajo presión crítica (es decir, por debajo de 22.1 MPa), pueden lograr una eficiencia de 36 a 40%. Diseños supercríticos, que funcionan a presión supercrítica(es decir, superior a 22.1 MPa), tienen eficiencias alrededor del 43%. Las centrales eléctricas de carbón más eficientes y también muy complejas que funcionan a presiones “ultra críticas” (es decir, alrededor de 30 MPa) y usan recalentamiento de etapas múltiples alcanzan aproximadamente el 48% de eficiencia.
Ver también: Reactor supercrítico
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.
