Facebook Instagram Youtube Twitter

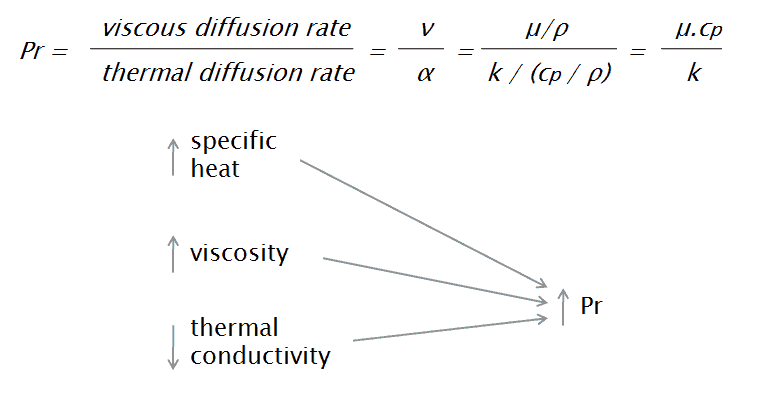
What is Prandtl Number Formula – Definition

by
Prandtl number is can be calculated as the ratio of momentum diffusivity to thermal diffusivity. Prandtl Number Formula – Equation

Prandtl Number

The Prandtl number is a dimensionless number, named after its inventor, a German engineer Ludwig Prandtl, who also identified the boundary layer. The Prandtl number is defined as the ratio of momentum diffusivity to thermal diffusivity. The momentum diffusivity, or as it is normally called, kinematic viscosity, tells us the material’s resistance to shear-flows (different layers of the flow travel with different velocities due to e.g. different speeds of adjacent walls) in relation to density. That is, the Prandtl number formula is given as:

Prandtl Number

where:

ν is momentum diffusivity (kinematic viscosity) [m2/s]

α is thermal diffusivity [m2/s]

μ is dynamic viscosity [N.s/m2]

k is thermal conductivity [W/m.K]

cp is specific heat [J/kg.K]

ρ is density [kg/m3]

Small values of the Prandtl number, Pr << 1, means the thermal diffusivity dominates. Whereas with large values, Pr >> 1, the momentum diffusivity dominates the behavior. For example, the typical value for liquid mercury, which is about 0.025, indicates that the heat conduction is more significant compared to convection, so thermal diffusivity is dominant. When Pr is small, it means that the heat diffuses quickly compared to the velocity.

In comparison to Reynolds number, the Prandtl number is not dependent on geometry of an object involved in the problem, but is dependent solely on the fluid and the fluid state. As such, the Prandtl number is often found in property tables alongside other properties such as viscosity and thermal conductivity.

 
References:
Heat Transfer:
  1. Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
  2. Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
  3. Fundamentals of Heat and Mass Transfer. C. P. Kothandaraman. New Age International, 2006, ISBN: 9788122417722.
  4. U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.

Nuclear and Reactor Physics:

  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Prandtl Number

We hope, this article, Prandtl Number Formula, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts