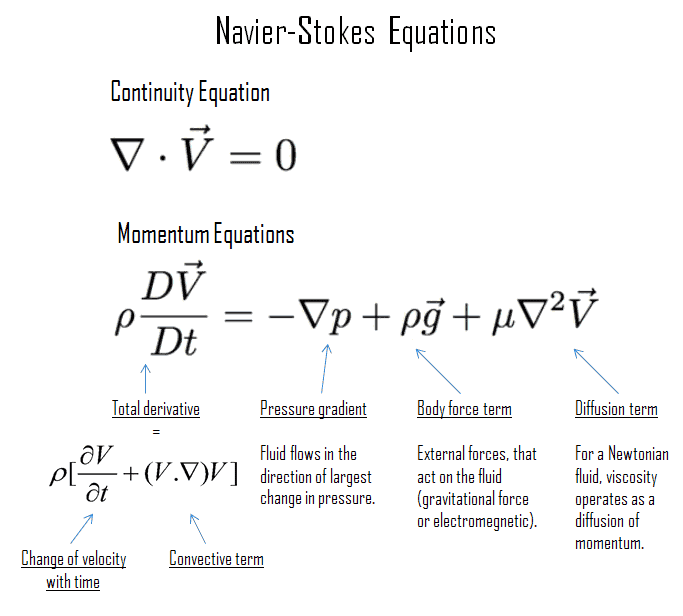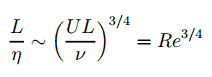Navier-Stokes-Gleichungen
In der Fluiddynamik , die Navier-Stokes – Gleichungen sind Gleichungen, welche die beschreiben dreidimensionale Bewegung von viskosen Flüssigkeit Substanzen. Diese Gleichungen sind nach Claude-Louis Navier (1785-1836) und George Gabriel Stokes (1819-1903) benannt. In Situationen, in denen das Fluid keine starken Temperaturgradienten aufweist, liefern diese Gleichungen eine sehr gute Annäherung an die Realität .
Die Navier-Stokes-Gleichungen bestehen aus einer zeitabhängigen Kontinuitätsgleichung zur Massenerhaltung , drei zeitabhängigen Erhaltungssätzen für Impulsgleichungen und einer zeitabhängigen Erhaltungssätzen für Energie . Es gibt vier unabhängige Variablen in dem Problem, die x-, y- und z-Raumkoordinaten einer Domäne und die Zeit t.
Wie zu sehen ist, sind die Navier-Stokes-Gleichungen nichtlineare partielle Differentialgleichungen zweiter Ordnung. Ihre Lösungen wurden für eine Vielzahl von interessanten Problemen mit viskoser Strömung gefunden. Sie können verwendet werden, um das Wetter, die Meeresströmungen, die Luftströmung um ein Strömungsprofil und die Wasserströmung in einem Rohr oder in einem Reaktor zu modellieren. Die Navier-Stokes-Gleichungen in ihrer vollständigen und vereinfachten Form helfen beim Entwurf von Flugzeugen und Autos, beim Studium des Blutflusses, beim Entwurf von Kernreaktoren und vielen anderen Dingen.
Lösung von Navier-Stokes-Gleichungen
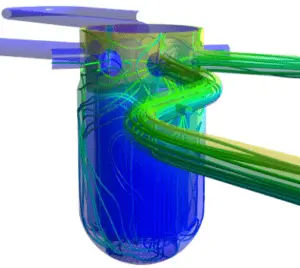
Quelle: CFD-Entwicklungsgruppe – hzdr.de
Obwohl die Navier-Stokes-Gleichungen nur eine begrenzte Anzahl bekannter analytischer Lösungen aufweisen, sind sie für eine feinmaschige Computermodellierung geeignet. Das Hauptwerkzeug für ihre Analyse ist die CFD-Analyse . CFD ist ein Zweig der Strömungsmechanik, der numerische Analysen und Algorithmen verwendet, um Probleme zu lösen und zu analysieren, die turbulente Strömungen betreffen. Es ist allgemein anerkannt, dass die Navier-Stokes-Gleichungen (oder die vereinfachten Reynolds-gemittelten Navier-Stokes-Gleichungen ) turbulente Lösungen aufweisen können, und diese Gleichungen sind die Grundlage für im Wesentlichen alle CFD-Codes. Es ist jetzt möglich, ungefähre, aber realistische CFD-Ergebnisse für eine Vielzahl komplexer zwei- und dreidimensionaler viskoser Strömungen zu erzielen.
Auch rein mathematisch sind die Navier-Stokes-Gleichungen von großem Interesse. Leider erschwert der stark intermittierende und unregelmäßige Charakter der turbulenten Strömung alle Analysen . Es ist noch nicht bewiesen, dass dreidimensionale Lösungen immer existieren oder dass sie glatt sind, wenn sie existieren. Tatsächlich wird die allgemeine Lösung der Navier-Stokes-Gleichungen mit Turbulenzen oft als “letztes ungelöstes Problem in der klassischen mathematischen Physik” bezeichnet.
Eigenschaften der turbulenten Strömung
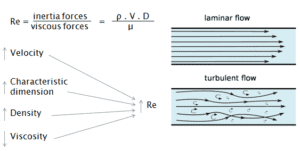Turbulente Strömung tritt tendenziell bei höheren Geschwindigkeiten , niedriger Viskosität und höheren charakteristischen linearen Abmessungen auf .- Wenn die Reynoldszahl größer als Re> 3500 ist, ist die Strömung turbulent.
- Unregelmäßigkeit: Die Strömung ist durch die unregelmäßige Bewegung von Partikeln der Flüssigkeit gekennzeichnet. Die Bewegung von Flüssigkeitsteilchen ist chaotisch. Aus diesem Grund wird turbulente Strömung normalerweise eher statistisch als deterministisch behandelt.
- Diffusivität: Bei turbulenter Strömung besteht eine relativ flache Geschwindigkeitsverteilung über den Rohrabschnitt, so dass die gesamte Flüssigkeit mit einem bestimmten Einzelwert fließt und extrem nahe an den Wänden schnell abfällt. Die Eigenschaft, die für das verbesserte Mischen und die erhöhten Raten von Massen-, Impuls- und Energietransporten in einer Strömung verantwortlich ist, wird als „Diffusionsvermögen“ bezeichnet.
- Rotation: Turbulente Strömung ist durch einen starken dreidimensionalen Wirbelerzeugungsmechanismus gekennzeichnet. Dieser Mechanismus ist als Wirbelstreckung bekannt.
- Dissipation: Ein dissipativer Prozess ist ein Prozess, bei dem die kinetische Energie der turbulenten Strömung durch viskose Scherbeanspruchung in innere Energie umgewandelt wird.
Kolmogorov Microscales
Nach Ansicht von Kolmogorov ( Andrey Nikolaevich Kolmogorov war ein russischer Mathematiker, der bedeutende Beiträge zur Mathematik der Wahrscheinlichkeitstheorie und der Turbulenzen geleistet hat) umfassen turbulente Bewegungen eine breite Palette von Skalen . Von einer Makroskala, in der die Energie zugeführt wird, zu einer Mikroskala, in der Energie durch Viskosität abgeführt wird.
Stellen Sie sich zum Beispiel eine Cumuluswolke vor. Die Makroskala der Wolke kann in der Größenordnung von Kilometern liegen und über lange Zeiträume wachsen oder bestehen bleiben. Innerhalb der Wolke können Wirbel über Skalen in der Größenordnung von Millimetern auftreten . Für kleinere Strömungen wie in Rohren können die Mikroskalen viel kleiner sein. Der größte Teil der kinetischen Energie der turbulenten Strömung ist in den makroskaligen Strukturen enthalten. Die Energie „kaskadiert“ durch einen Trägheitsmechanismus von diesen makroskaligen Strukturen zu mikroskaligen Strukturen. Dieser Prozess ist als turbulente Energiekaskade bekannt .
Die kleinsten Skalen in turbulenten Strömungen sind als Kolmogorov-Mikroskalen bekannt . Diese sind klein genug, dass die molekulare Diffusion wichtig wird und eine viskose Energiedissipation stattfindet und die turbulente kinetische Energie in Wärme umgewandelt wird.
Die kleinsten Skalen in turbulenter Strömung, dh die Kolmogorov-Mikroskalen, sind:
Dabei ist ε die durchschnittliche Dissipationsrate der kinetischen Turbulenzenergie pro Masseneinheit und hat Abmessungen (m 2 / s 3 ). ν ist die kinematische Viskosität des Fluids und hat Abmessungen (m 2 / s).
Die Größe des kleinsten Wirbels in der Strömung wird durch die Viskosität bestimmt. Die Kolmogorov- Längenskala nimmt mit abnehmender Viskosität ab. Bei Flüssen mit sehr hoher Reynoldszahl sind die viskosen Kräfte im Verhältnis zu den Trägheitskräften geringer. Bewegungen in kleinerem Maßstab werden dann notwendigerweise erzeugt, bis die Auswirkungen der Viskosität wichtig werden und Energie abgeführt wird. Das Verhältnis der größten zu den kleinsten Längenskalen in der turbulenten Strömung ist proportional zur Reynolds-Zahl (erhöht sich mit der Dreiviertelleistung ).
Dies führt dazu, dass direkte numerische Simulationen turbulenter Strömungen praktisch unmöglich sind. Betrachten Sie beispielsweise einen Fluss mit einer Reynolds-Zahl von 10 6 . In diesem Fall ist das Verhältnis L / l proportional zu 10 18/4 . Da wir das dreidimensionale Problem analysieren müssen, müssen wir ein Gitter berechnen, das aus mindestens 10 14 Gitterpunkten besteht . Dies übertrifft die Kapazität und die Möglichkeiten vorhandener Computer bei weitem.
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.
