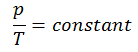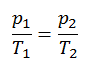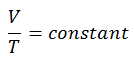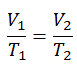Ciclo de Atkinson – Atkinson Engine
Em 1882, um engenheiro britânico, James Atkinson, avançou no estudo de motores térmicos, inventando vários motores térmicos que tiveram uma eficiência aumentada ao longo do ciclo Otto . Isso foi alcançado com o uso de cursos de motor variáveis de um eixo de manivela complexo. O ciclo de Atkinson foi projetado para fornecer maior eficiência às custas da densidade de potência. Para dois motores de igual volume de cilindrada, aquele com ciclo Otto produziria o maior trabalho líquido e, se os motores funcionassem na mesma velocidade, maior potência. Por outro lado, o ciclo de Atkinson teria maior eficiência térmica e, portanto, menor consumo de combustível.
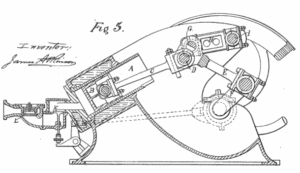
A primeira implementação do ciclo de Atkinson foi em 1882. Esse mecanismo é conhecido como o ” Diferencial de 1882 “. Foi organizado como um motor de pistão oposto, o motor diferencial de Atkinson. O próximo mecanismo projetado por Atkinson em 1887 foi nomeado ” Motor de Ciclo ” (veja a figura)
Recentemente, é um dos ciclos termodinâmicos que podem ser encontrados em motores de automóveis e descreve o funcionamento de um motor de pistão de ignição por faísca . O termo ciclo de Atkinson foi usado para descrever um motor de ciclo Otto modificado no qual a válvula de admissão é mantida aberta por mais tempo do que o normal para permitir um fluxo reverso de ar de admissão no coletor de admissão. Isso reduz a taxa de compactação , mas a taxa de expansão permanece a mesma. Do ponto de vista mecânico, o motor Atkinson é semelhante ao motor Otto. A principal diferença está na árvore de cames ou nas árvores de cames.
Ciclo de Atkinson – Processos
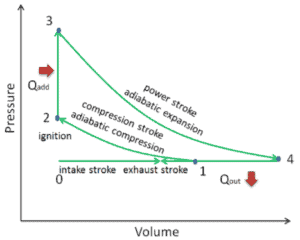
Em um ciclo de Atkinson ( ciclo Otto modificado), o sistema que executa o ciclo passa por uma série de quatro processos: dois processos isentrópicos (adiabáticos reversíveis) alternados com um processo isocórico e um processo isobárico:
- Compressão isentrópica (curso de compressão) – O gás (mistura combustível-ar) é comprimido adiabaticamente do estado 1 ao estado 2, à medida que o pistão se move do ponto de fechamento da válvula de admissão (1) para o ponto morto superior. O ambiente trabalha com o gás, aumentando sua energia interna (temperatura) e comprimindo-o. Por outro lado, a entropia permanece inalterada. As mudanças nos volumes e sua proporção ( V 1 / V 2 ) são conhecidas como taxa de compressão . A taxa de compactação é menor que a taxa de expansão.
- Compressão isocórica (fase de ignição) – Nesta fase (entre o estado 2 e o estado 3), há um volume constante (o pistão está em repouso) transferido para o ar a partir de uma fonte externa, enquanto o pistão está em repouso no ponto morto superior . Este processo é semelhante ao processo isocórico no ciclo Otto. Pretende-se representar a ignição da mistura combustível-ar injetada na câmara e a subsequente queima rápida. A pressão aumenta e a razão ( P 3 / P 2 ) é conhecida como “taxa de explosão”.
- Expansão isentrópica (golpe de energia) – O gás se expande adiabaticamente do estado 3 para o estado 4, conforme o pistão se move do ponto morto superior para o ponto morto inferior. O gás trabalha nos arredores (pistão) e perde uma quantidade de energia interna igual ao trabalho que sai do sistema. Novamente a entropia permanece inalterada. A taxa de volume ( V 4 / V 3 ) é conhecida como taxa de expansão isentrópica.
- Exaustão isobárica (curso de exaustão) – O objetivo principal do ciclo moderno de Atkinson é permitir que a pressão na câmara de combustão no final do curso de potência seja igual à pressão atmosférica. Como pode haver pressão atmosférica na câmara, não há descompressão como no ciclo Otto. O pistão se move do ponto morto inferior (BDC) para o ponto morto superior (TDC) e o ciclo passa pelos pontos 4 → 1 → 0. Nesse curso, a válvula de escape está aberta enquanto o pistão puxa os gases de escape para fora da câmara.
Durante o ciclo de Atkinson , o trabalho é realizado no gás pelo pistão entre os estados 1 e 2 ( compressão isentrópica ). O trabalho é realizado pelo gás no pistão entre os estágios 3 e 4 ( expansão isentrópica ). A diferença entre o trabalho realizado pelo gás e o trabalho realizado com o gás é o trabalho líquido produzido pelo ciclo e corresponde à área delimitada pela curva do ciclo. O trabalho produzido pelos tempos de ciclo, a taxa do ciclo (ciclos por segundo) é igual à potência produzida pelo motor Atkinson.
Processo isentrópico
Um processo isentrópico é um processo termodinâmico , no qual a entropia do fluido ou gás permanece constante. Isso significa que o processo isentrópico é um caso especial de um processo adiabático no qual não há transferência de calor ou matéria. É um processo adiabático reversível . A suposição de que não há transferência de calor é muito importante, pois podemos usar a aproximação adiabática apenas em processos muito rápidos .
Processo isentrópico e a primeira lei
Para um sistema fechado, podemos escrever a primeira lei da termodinâmica em termos de entalpia :
dH = dQ + Vdp
ou
dH = TdS + Vdp
Processo isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C P (T 2 – T 1 ) (para gás ideal )
Processo isentrópico do gás ideal
O processo isentrópico (um caso especial de processo adiabático) pode ser expresso com a lei dos gases ideais como:
pV κ = constante
ou
p 1 V 1 k = p 2 V 2 k
em que κ = c p / c v é a proporção de aquecimentos específicos (ou capacidades de calor ) para o gás. Um para pressão constante (c p ) e outro para volume constante (c v ) . Observe que essa razão κ = c p / c v é um fator na determinação da velocidade do som em um gás e em outros processos adiabáticos.
Processo Isocórico
Um processo isocórico é um processo termodinâmico, no qual o volume do sistema fechado permanece constante (V = const). Ele descreve o comportamento do gás dentro do recipiente, que não pode ser deformado. Como o volume permanece constante, a transferência de calor para dentro ou para fora do sistema não funciona , mas altera apenas a energia interna (a temperatura) do sistema.
Processo isocórico e a primeira lei
A forma clássica da primeira lei da termodinâmica é a seguinte equação:
dU = dQ – dW
Nesta equação, dW é igual a dW = pdV e é conhecido como trabalho de fronteira . Então:
dU = dQ – pdV
No processo isocórico e no gás ideal , todo o calor adicionado ao sistema será usado para aumentar a energia interna.
Processo isocórico (pdV = 0):
dU = dQ (para gás ideal)
dU = 0 = Q – W → W = Q (para gás ideal)
Processo isocórico do gás ideal
O processo isocórico pode ser expresso com a lei dos gases ideais como:
ou
Em um diagrama pV , o processo ocorre ao longo de uma linha horizontal que possui a equação V = constante.
Veja também: Lei de Guy-Lussac
Processo isobárico
Um processo isobárico é um processo termodinâmico , no qual a pressão do sistema permanece constante (p = const). A transferência de calor para dentro ou para fora do sistema funciona, mas também altera a energia interna do sistema.
Como existem mudanças na energia interna (dU) e no volume do sistema (∆V), os engenheiros costumam usar a entalpia do sistema, que é definida como:
H = U + pV
Processo isobárico e a primeira lei
A forma clássica da primeira lei da termodinâmica é a seguinte equação:
dU = dQ – dW
Nesta equação, dW é igual a dW = pdV e é conhecido como trabalho de fronteira . Em um processo isobárico e no gás ideal, parte do calor adicionado ao sistema será usada para realizar o trabalho e parte do calor adicionado aumentará a energia interna (aumentará a temperatura). Portanto, é conveniente usar a entalpia em vez da energia interna.
Processo isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Na entropia constante , ou seja, no processo isentrópico, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no sistema ou pelo mesmo.
Processo isobárico do gás ideal
O processo isobárico pode ser expresso com a lei do gás ideal como:
ou
Em um diagrama de pV , o processo ocorre ao longo de uma linha horizontal (chamada isobar) que possui a equação p = constante.
Veja também: Lei de Charles
Eficiência térmica para o ciclo de Atkinson
Em geral, a eficiência térmica , η th , de qualquer motor de calor é definida como a razão entre o trabalho que faz, W , para o calor de entrada a uma temperatura elevada, Q H .
A eficiência térmica , η th , representa a fração de calor , Q H , que é convertida em trabalho . Como a energia é conservada de acordo com a primeira lei da termodinâmica e a energia não pode ser convertida para funcionar completamente, a entrada de calor, Q H , deve ser igual ao trabalho realizado, W, mais o calor que deve ser dissipado como calor residual Q C no meio Ambiente. Portanto, podemos reescrever a fórmula da eficiência térmica como:
O calor absorvido ocorre durante a combustão da mistura combustível-ar, quando a faísca ocorre, aproximadamente a volume constante. Como durante um processo isocórico não há trabalho realizado pelo sistema ou sobre ele, a primeira lei da termodinâmica determina ∆U = ∆Q.
Portanto, o calor adicionado e rejeitado é dado por:
Q add = mc v (T 3 – T 2 )
Q out = mc p (T 4 – T 1 )
Substituindo essas expressões pelo calor adicionado e rejeitado na expressão por eficiência térmica, obtém-se:
Além disso, pode-se derivar isso em termos de:
- a razão V 1 / V 2 , que é conhecida como taxa de compressão – CR
- a razão V 4 / V 3 , que é conhecida como taxa de expansão – ER.
- κ = c p / c v
A expressão para eficiência térmica usando essas características é:
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.