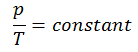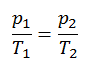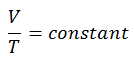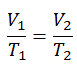Ciclo Atkinson – Motor Atkinson
En 1882, un ingeniero británico, James Atkinson, avanzó en el estudio de los motores térmicos al inventar varios motores térmicos que tienen una mayor eficiencia durante el ciclo Otto . Esto se logró mediante el uso de movimientos variables del motor de un cigüeñal complejo. El ciclo Atkinson está diseñado para proporcionar una mayor eficiencia a expensas de la densidad de potencia. Para dos motores de igual volumen de desplazamiento, el que tiene un ciclo Otto produciría el mayor trabajo neto y, si los motores funcionan a la misma velocidad, mayor potencia. Por otro lado, el ciclo Atkinson tendría una mayor eficiencia térmica y, por lo tanto, un menor consumo de combustible.
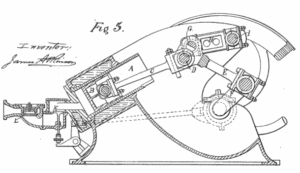
La primera implementación del ciclo Atkinson fue en 1882. Este motor se conoce como el ” Diferencial 1882 “. Estaba dispuesto como un motor de pistón opuesto, el motor diferencial Atkinson. El siguiente motor diseñado por Atkinson en 1887 se denominó ” Cycle Engine ” (ver figura)
Recientemente, es uno de los ciclos termodinámicos que se pueden encontrar en los motores de automóviles y describe el funcionamiento de un motor de pistón de encendido por chispa . El término ciclo de Atkinson se ha utilizado para describir un motor de ciclo Otto modificado en el que la válvula de admisión se mantiene abierta durante más tiempo de lo normal para permitir un flujo inverso de aire de admisión en el colector de admisión. Esto reduce la relación de compresión , pero la relación de expansión sigue siendo la misma. Desde un punto de vista mecánico, el motor Atkinson es similar al motor Otto. La principal diferencia está en el árbol de levas o árboles de levas.
Ciclo Atkinson – Procesos
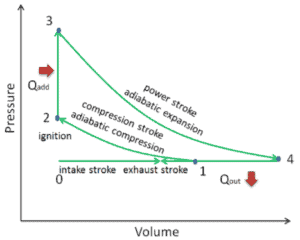
En un ciclo Atkinson ( ciclo Otto modificado), el sistema que ejecuta el ciclo se somete a una serie de cuatro procesos: dos procesos isentrópicos (adiabáticos reversibles) alternados con un proceso isocrórico y un proceso isobárico:
- Compresión isentrópica (carrera de compresión): el gas (mezcla de combustible y aire) se comprime adiabáticamente desde el estado 1 al estado 2, a medida que el pistón se mueve desde el punto de cierre de la válvula de admisión (1) hasta el punto muerto superior. Los alrededores trabajan con el gas, aumentando su energía interna (temperatura) y comprimiéndolo. Por otro lado, la entropía permanece sin cambios. Los cambios en los volúmenes y su relación ( V 1 / V 2 ) se conocen como la relación de compresión . La relación de compresión es menor que la relación de expansión.
- Compresión isocórica (fase de encendido): en esta fase (entre el estado 2 y el estado 3) hay una transferencia de calor de volumen constante (el pistón está en reposo) al aire desde una fuente externa mientras el pistón está en reposo en el punto muerto superior . Este proceso es similar al proceso isocrórico en el ciclo de Otto. Su objetivo es representar el encendido de la mezcla de combustible y aire inyectada en la cámara y la posterior combustión rápida. La presión aumenta y la relación ( P 3 / P 2 ) se conoce como la “relación de explosión”.
- Expansión isentrópica (golpe de poder): el gas se expande adiabáticamente desde el estado 3 al estado 4, a medida que el pistón se mueve desde el punto muerto superior al punto muerto inferior. El gas funciona en el entorno (pistón) y pierde una cantidad de energía interna igual al trabajo que abandona el sistema. Nuevamente, la entropía permanece sin cambios. La relación de volumen ( V 4 / V 3 ) se conoce como la relación de expansión isentrópica.
- Escape isobárico (carrera de escape) : el objetivo principal del ciclo moderno de Atkinson es permitir que la presión en la cámara de combustión al final de la carrera de potencia sea igual a la presión atmosférica. Como puede haber presión atmosférica en la cámara, no hay descompresión como en un ciclo Otto. El pistón se mueve desde el punto muerto inferior (BDC) al punto muerto superior (TDC) y el ciclo pasa los puntos 4 → 1 → 0. En esta carrera, la válvula de escape está abierta mientras el pistón extrae los gases de escape de la cámara.
Durante el ciclo de Atkinson , el pistón trabaja en el gas entre los estados 1 y 2 ( compresión isentrópica ). El gas realiza el trabajo en el pistón entre las etapas 3 y 4 ( expansión isentrópica ). La diferencia entre el trabajo realizado por el gas y el trabajo realizado sobre el gas es el trabajo neto producido por el ciclo y corresponde al área encerrada por la curva del ciclo. El trabajo producido por el ciclo multiplicado por la velocidad del ciclo (ciclos por segundo) es igual a la potencia producida por el motor Atkinson.
Proceso isentrópico
Un proceso isentrópico es un proceso termodinámico , en el cual la entropía del fluido o gas permanece constante. Significa que el proceso isentrópico es un caso especial de un proceso adiabático en el que no hay transferencia de calor o materia. Es un proceso adiabático reversible . La suposición de que no hay transferencia de calor es muy importante, ya que podemos usar la aproximación adiabática solo en procesos muy rápidos .
Proceso isentrópico y la primera ley
Para un sistema cerrado, podemos escribir la primera ley de la termodinámica en términos de entalpía :
dH = dQ + Vdp
o
dH = TdS + Vdp
Proceso isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 ) (para gas ideal )
Proceso isentrópico del gas ideal
El proceso isentrópico (un caso especial de proceso adiabático) se puede expresar con la ley de los gases ideales como:
pV κ = constante
o
p 1 V 1 κ = p 2 V 2 κ
en el que κ = c p / c v es la relación de los calores específicos (o capacidades de calor ) para el gas. Uno para presión constante (c p ) y otro para volumen constante (c v ) . Tenga en cuenta que esta relación κ = c p / c v es un factor para determinar la velocidad del sonido en un gas y otros procesos adiabáticos.
Proceso isocorico
Un proceso isocrórico es un proceso termodinámico, en el que el volumen del sistema cerrado permanece constante (V = constante). Describe el comportamiento del gas dentro del contenedor, que no puede deformarse. Como el volumen permanece constante, la transferencia de calor dentro o fuera del sistema no funciona con el p∆V , sino que solo cambia la energía interna (la temperatura) del sistema.
Proceso isocrórico y la primera ley
La forma clásica de la primera ley de la termodinámica es la siguiente ecuación:
dU = dQ – dW
En esta ecuación, dW es igual a dW = pdV y se conoce como el trabajo límite . Luego:
dU = dQ – pdV
En el proceso isocrórico y el gas ideal , todo el calor agregado al sistema se utilizará para aumentar la energía interna.
Proceso isocórico (pdV = 0):
dU = dQ (para gas ideal)
dU = 0 = Q – W → W = Q (para gas ideal)
Proceso isocrórico del gas ideal
El proceso isocrórico se puede expresar con la ley de los gases ideales como:
o
En un diagrama pV , el proceso ocurre a lo largo de una línea horizontal que tiene la ecuación V = constante.
Ver también: Ley de Guy-Lussac
Proceso isobárico
Un proceso isobárico es un proceso termodinámico , en el cual la presión del sistema permanece constante (p = const). La transferencia de calor dentro o fuera del sistema funciona, pero también cambia la energía interna del sistema.
Dado que hay cambios en la energía interna (dU) y cambios en el volumen del sistema (∆V), los ingenieros a menudo usan la entalpía del sistema, que se define como:
H = U + pV
Proceso isobárico y la primera ley
La forma clásica de la primera ley de la termodinámica es la siguiente ecuación:
dU = dQ – dW
En esta ecuación, dW es igual a dW = pdV y se conoce como el trabajo límite . En un proceso isobárico y el gas ideal, parte del calor agregado al sistema se utilizará para hacer el trabajo y parte del calor agregado aumentará la energía interna (aumentará la temperatura). Por lo tanto, es conveniente utilizar la entalpía en lugar de la energía interna.
Proceso isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
En una entropía constante , es decir, en un proceso isentrópico, el cambio de entalpía equivale al trabajo del proceso de flujo realizado en o por el sistema.
Proceso isobárico del gas ideal
El proceso isobárico se puede expresar con la ley de los gases ideales como:
o
En un diagrama pV , el proceso ocurre a lo largo de una línea horizontal (llamada isobar) que tiene la ecuación p = constante.
Ver también: Ley de Charles
Eficiencia térmica para el ciclo de Atkinson
En general, la eficiencia térmica , η º , de cualquier motor de calor se define como la relación de la obra lo hace, W , para el calor de entrada a la alta temperatura, Q H .
La eficiencia térmica , η th , representa la fracción de calor , Q H , que se convierte en trabajo . Dado que la energía se conserva de acuerdo con la primera ley de la termodinámica y la energía no se puede convertir en trabajo por completo, la entrada de calor, Q H , debe ser igual al trabajo realizado, W, más el calor que se debe disipar como calor residual Q C en el ambiente. Por lo tanto, podemos reescribir la fórmula para la eficiencia térmica como:
El calor absorbido ocurre durante la combustión de la mezcla de combustible y aire, cuando se produce la chispa, aproximadamente a un volumen constante. Dado que durante un proceso isocrórico no hay trabajo realizado por o sobre el sistema, la primera ley de la termodinámica dicta ∆U = ∆Q.
Por lo tanto, el calor agregado y rechazado están dados por:
Q add = mc v (T 3 – T 2 )
Q out = mc p (T 4 – T 1 )
Sustituyendo estas expresiones por el calor agregado y rechazado en la expresión por rendimientos de eficiencia térmica:
Además, se puede deducir que en términos de:
- la relación V 1 / V 2 , que se conoce como la relación de compresión – CR
- la relación V 4 / V 3 , que se conoce como la relación de expansión – ER.
- κ = c p / c v
La expresión para la eficiencia térmica usando estas características es:
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.