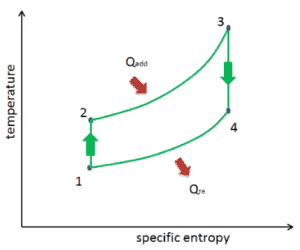
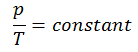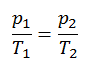Ciclo de Carnot – pV, diagrama Ts
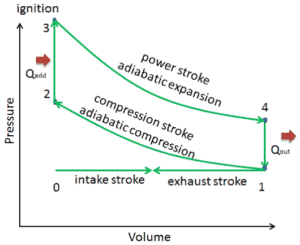
El ciclo de Otto a menudo se representa en un diagrama de presión-volumen (diagrama pV ) y en un diagrama de temperatura-entropía (diagrama Ts). Cuando se traza en un diagrama de volumen de presión, los procesos isocróricos siguen las líneas isocróricas para el gas (las líneas verticales), los procesos adiabáticos se mueven entre estas líneas verticales y el área delimitada por la ruta completa del ciclo representa el trabajo total que se puede hacer durante uno ciclo.
El diagrama de temperatura-entropía (diagrama Ts ) en el que el estado termodinámico se especifica mediante un punto en un gráfico con entropía específica (s) como eje horizontal y temperatura absoluta (T) como eje vertical. Los diagramas Ts son una herramienta útil y común, particularmente porque ayuda a visualizar la transferencia de calor durante un proceso. Para procesos reversibles (ideales), el área bajo la curva Ts de un proceso es el calor transferido al sistema durante ese proceso.
Proceso isentrópico
Un proceso isentrópico es un proceso termodinámico , en el cual la entropía del fluido o gas permanece constante. Significa que el proceso isentrópico es un caso especial de un proceso adiabático en el que no hay transferencia de calor o materia. Es un proceso adiabático reversible . La suposición de que no hay transferencia de calor es muy importante, ya que podemos usar la aproximación adiabática solo en procesos muy rápidos .
Proceso isentrópico y la primera ley
Para un sistema cerrado, podemos escribir la primera ley de la termodinámica en términos de entalpía :
dH = dQ + Vdp
o
dH = TdS + Vdp
Proceso isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 ) (para gas ideal )
Proceso isentrópico del gas ideal
El proceso isentrópico (un caso especial de proceso adiabático) se puede expresar con la ley de los gases ideales como:
pV κ = constante
o
p 1 V 1 κ = p 2 V 2 κ
en el que κ = c p / c v es la relación de los calores específicos (o capacidades de calor ) para el gas. Uno para presión constante (c p ) y otro para volumen constante (c v ) . Tenga en cuenta que esta relación κ = c p / c v es un factor para determinar la velocidad del sonido en un gas y otros procesos adiabáticos.
Proceso isotérmico
Un proceso isocrórico es un proceso termodinámico, en el que el volumen del sistema cerrado permanece constante (V = constante). Describe el comportamiento del gas dentro del contenedor, que no puede deformarse. Como el volumen permanece constante, la transferencia de calor dentro o fuera del sistema no funciona con el p∆V , sino que solo cambia la energía interna (la temperatura) del sistema.
Proceso isocrórico y la primera ley
La forma clásica de la primera ley de la termodinámica es la siguiente ecuación:
dU = dQ – dW
En esta ecuación, dW es igual a dW = pdV y se conoce como el trabajo límite . Luego:
dU = dQ – pdV
En el proceso isocrórico y el gas ideal , todo el calor agregado al sistema se utilizará para aumentar la energía interna.
Proceso isocórico (pdV = 0):
dU = dQ (para gas ideal)
dU = 0 = Q – W → W = Q (para gas ideal)
Proceso isocrórico del gas ideal
El proceso isocrórico se puede expresar con la ley de los gases ideales como:
o
En un diagrama pV , el proceso ocurre a lo largo de una línea horizontal que tiene la ecuación V = constante.
Ver también: Ley de Guy-Lussac
Comparación de los ciclos reales e ideales de Otto
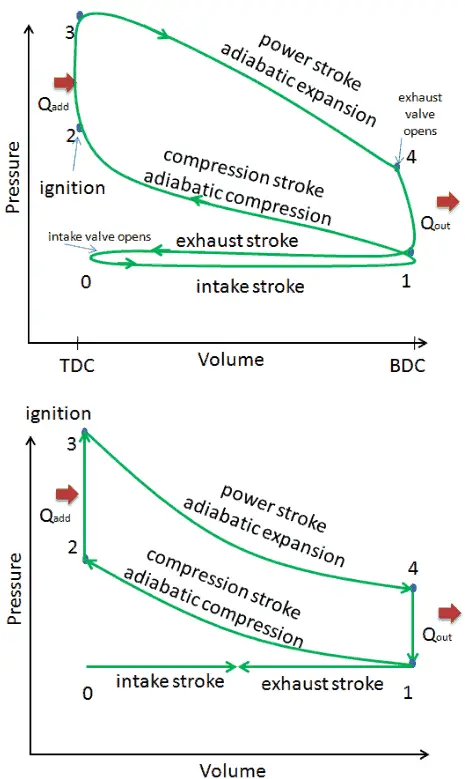En esta sección, se muestra un ciclo ideal de Otto en el que hay muchos supuestos que difieren del ciclo real de Otto . Las principales diferencias entre el motor Otto real e ideal aparecen en la figura. En realidad, el ciclo ideal no ocurre y hay muchas pérdidas asociadas con cada proceso. Para un ciclo real, la forma del diagrama pV es similar al ideal, pero el área (trabajo) encerrada en el diagrama pV siempre es menor que el valor ideal. El ciclo ideal de Otto se basa en los siguientes supuestos:
- Ciclo cerrado. La mayor diferencia entre los dos diagramas es la simplificación de las carreras de admisión y escape en el ciclo ideal. En la carrera de escape, el calor Q a cabo se expulsa al medio ambiente, en un motor real, las hojas de gas del motor y se sustituye por una nueva mezcla de aire y combustible.
- Adición de calor instantáneo (adición de calor isocrórico). En los motores reales, la adición de calor no es instantánea, por lo tanto, la presión máxima no está en TDC, sino justo después de TDC.
- Sin transferencia de calor (adiabático)
- Compresión: el gas (mezcla de combustible y aire) se comprime adiabáticamente del estado 1 al estado 2. En los motores reales, siempre hay algunas ineficiencias que reducen la eficiencia térmica.
- Expansión. El gas (mezcla de combustible y aire) se expande adiabáticamente del estado 3 al estado 4.
- Combustión completa de la mezcla de combustible y aire.
- Sin trabajo de bombeo . El trabajo de bombeo es la diferencia entre el trabajo realizado durante la carrera de escape y el trabajo realizado durante la carrera de admisión. En ciclos reales, hay una diferencia de presión entre las presiones de escape y de entrada.
- Sin pérdida por purga . La pérdida por purga es causada por la apertura temprana de las válvulas de escape. Esto da como resultado una pérdida de producción de trabajo durante la carrera de expansión.
- Sin pérdidas por golpe . La pérdida por soplado es causada por la fuga de gases comprimidos a través de anillos de pistón y otras grietas.
- Sin pérdidas por fricción .
Estos supuestos y pérdidas simplificadores conducen al hecho de que el área cerrada (trabajo) del diagrama pV para un motor real es significativamente menor que el tamaño del área (trabajo) encerrada en el diagrama pV del ciclo ideal. En otras palabras, el ciclo ideal del motor sobreestimará el trabajo neto y, si los motores funcionan a la misma velocidad, una mayor potencia producida por el motor real en aproximadamente un 20%.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.
