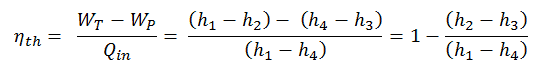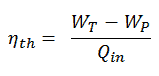Teoría de las turbinas de vapor – Termodinámica
En 1859, un ingeniero escocés, William John Macquorn Rankine, avanzó en el estudio de los motores térmicos al publicar el ” Manual del motor de vapor y otros motores principales “. Rankine desarrolló una teoría completa de la máquina de vapor y, de hecho, de todas las máquinas de calor. Junto con Rudolf Clausius y William Thomson (Lord Kelvin), contribuyó a la termodinámica, centrándose particularmente en la primera de las tres leyes termodinámicas.
El ciclo de Rankine lleva su nombre y describe el rendimiento de los sistemas de turbinas de vapor , aunque el principio teórico también se aplica a motores alternativos como las locomotoras de vapor. En general, el ciclo de Rankine es un ciclo termodinámico idealizado de un motor térmico de presión constante que convierte parte del calor en trabajo mecánico. En este ciclo, el calor se suministra externamente a un circuito cerrado, que generalmente usa agua (en fase líquida y de vapor) como fluido de trabajo. En contraste con el ciclo de Brayton , el fluido de trabajo en el ciclo de Rankine experimenta el cambio de fase de una fase líquida a una de vapor y viceversa.
Si bien muchas sustancias podrían usarse como fluido de trabajo en el ciclo de Rankine (inorgánico o incluso orgánico), el agua suele ser el líquido de elección debido a sus propiedades favorables, como su química no tóxica y no reactiva, abundancia y bajo costo, así como sus propiedades termodinámicas. Por ejemplo, el agua tiene el calor específico más alto de cualquier sustancia común: 4,19 kJ / kg K. Además, tiene un calor de vaporización muy alto , lo que lo convierte en un refrigerante y medio efectivo en centrales térmicas y otras industrias energéticas. En el caso del ciclo de Rankine, la Ley del Gas Idealcasi no se puede usar (el vapor no sigue pV = nRT), por lo tanto, todos los parámetros importantes de agua y vapor se tabulan en las llamadas ” Tablas de vapor “.
Una de las principales ventajas del ciclo Rankine es que el proceso de compresión en la bomba tiene lugar en un líquido . Al condensar el vapor de trabajo en un líquido (dentro de un condensador), la presión en la salida de la turbina se reduce y la energía requerida por la bomba de alimentación consume solo del 1% al 3% de la potencia de salida de la turbina y estos factores contribuyen a una mayor eficiencia para el ciclo.
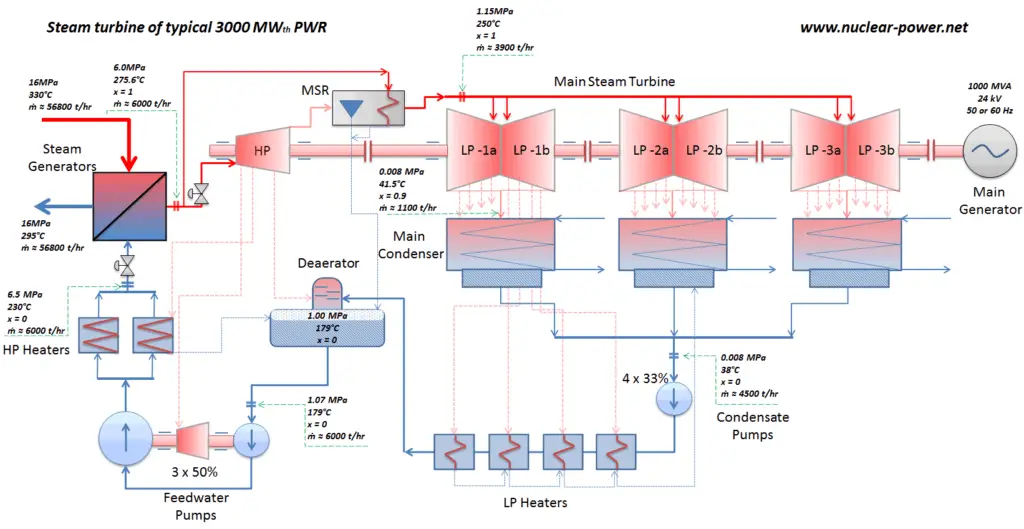
Hoy, el ciclo de Rankine es el ciclo operativo fundamental de todas las centrales térmicas donde un fluido operativo se evapora y condensa continuamente. Es uno de los ciclos termodinámicos más comunes , porque en la mayoría de los lugares del mundo la turbina funciona con vapor.
A diferencia del ciclo de Carnot, el ciclo de Rankine no ejecuta procesos isotérmicos, ya que estos deben realizarse muy lentamente. En un ciclo ideal de Rankine, el sistema que ejecuta el ciclo se somete a una serie de cuatro procesos: dos procesos isentrópicos (adiabáticos reversibles) alternados con dos procesos isobáricos.
Dado que el principio de Carnot establece que ningún motor puede ser más eficiente que un motor reversible ( un motor térmico de Carnot ) que opera entre los mismos depósitos de alta temperatura y baja temperatura, una turbina de vapor basada en el ciclo de Rankine debe tener una eficiencia menor que la eficiencia de Carnot.
En las centrales nucleares modernas, la eficiencia térmica general es de aproximadamente un tercio (33%), por lo que se necesitan 3000 MWth de energía térmica de la reacción de fisión para generar 1000 MWe de energía eléctrica. Se pueden lograr mayores eficiencias aumentando la temperatura del vapor . Pero esto requiere un aumento de las presiones dentro de las calderas o generadores de vapor.. Sin embargo, las consideraciones metalúrgicas ponen límites superiores a tales presiones. En comparación con otras fuentes de energía, la eficiencia térmica del 33% no es mucho. Pero debe tenerse en cuenta que las centrales nucleares son mucho más complejas que las centrales de combustibles fósiles y es mucho más fácil quemar combustibles fósiles que generar energía a partir de combustibles nucleares .
Ciclo Rankine – Procesos
En un ciclo ideal de Rankine, el sistema que ejecuta el ciclo se somete a una serie de cuatro procesos: dos procesos isentrópicos (adiabáticos reversibles) alternados con dos procesos isobáricos:
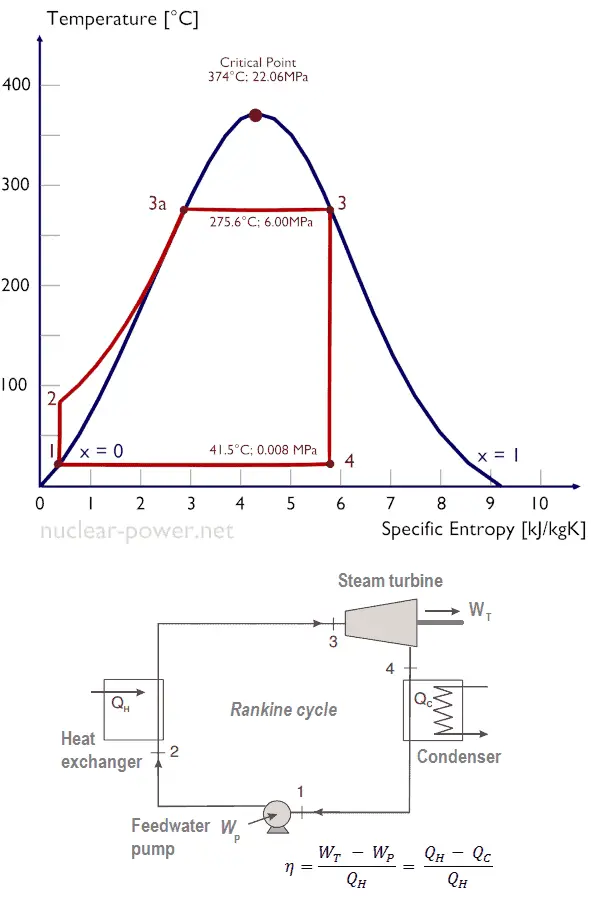Compresión isentrópica (compresión en bombas centrífugas): el condensado líquido se comprime adiabáticamente del estado 1 al estado 2 mediante bombas centrífugas (generalmente mediante bombas de condensado y luego mediante bombas de agua de alimentación). El condensado líquido se bombea desde el condensador a la caldera de mayor presión. En este proceso, los alrededores trabajan en el fluido, aumentando su entalpía (h = u + pv) y comprimiéndolo (aumentando su presión). Por otro lado, la entropía permanece sin cambios. El trabajo requerido para el compresor viene dado por W Pumps = H 2 – H 1 .- Adición de calor isobárico (en un intercambiador de calor – caldera): en esta fase (entre el estado 2 y el estado 3) hay una transferencia de calor a presión constante al condensado líquido desde una fuente externa, ya que la cámara está abierta para entrar y salir . El agua de alimentación (circuito secundario) se calienta desde el punto de ebullición (2 → 3a) de ese fluido y luego se evapora en la caldera (3a → 3). El calor neto agregado viene dado por Q add = H 3 – H 2
- Expansión isentrópica (expansión en una turbina de vapor): el vapor de la caldera se expande adiabáticamente desde el estado 3 al estado 4 en una turbina de vapor para producir trabajo y luego se descarga al condensador (parcialmente condensado). El vapor funciona en los alrededores (palas de la turbina) y pierde una cantidad de entalpía igual al trabajo que abandona el sistema. El trabajo realizado por la turbina viene dado por W T = H 4 – H 3 . Nuevamente, la entropía permanece sin cambios.
- Rechazo de calor isobárico (en un intercambiador de calor) : en esta fase, el ciclo se completa mediante un proceso de presión constante en el que se rechaza el calor del vapor parcialmente condensado. Hay una transferencia de calor del vapor al agua de enfriamiento que fluye en un circuito de enfriamiento. El vapor se condensa y la temperatura del agua de enfriamiento aumenta. El calor neto rechazado viene dado por Q re = H 4 – H 1
Durante un ciclo de Rankine, las bombas realizan el trabajo en el fluido entre los estados 1 y 2 ( i compresión sentrópica ). El fluido de la turbina realiza el trabajo entre las etapas 3 y 4 ( i expansión sentrópica ). La diferencia entre el trabajo realizado por el fluido y el trabajo realizado sobre el fluido es el trabajo neto producido por el ciclo y corresponde al área encerrada por la curva del ciclo (en el diagrama pV). El fluido de trabajo en un ciclo de Rankine sigue un ciclo cerrado y se reutiliza constantemente.
Como se puede ver, es conveniente utilizar la entalpía y la primera ley en términos de entalpía en el análisis de este ciclo termodinámico. Esta forma de ley simplifica la descripción de la transferencia de energía . A presión constante , el cambio de entalpía es igual a la energía transferida del ambiente a través del calentamiento:
Proceso isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
En una entropía constante , es decir, en un proceso isentrópico, el cambio de entalpía es igual al trabajo del proceso de flujo realizado en o por el sistema:
Proceso isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1
Ver también: ¿Por qué los ingenieros de energía usan la entalpía? Respuesta: dH = dQ + Vdp
Proceso isentrópico
Un proceso isentrópico es un proceso termodinámico , en el cual la entropía del fluido o gas permanece constante. Significa que el proceso isentrópico es un caso especial de un proceso adiabático en el que no hay transferencia de calor o materia. Es un proceso adiabático reversible . La suposición de que no hay transferencia de calor es muy importante, ya que podemos usar la aproximación adiabática solo en procesos muy rápidos .
Proceso isentrópico y la primera ley
Para un sistema cerrado, podemos escribir la primera ley de la termodinámica en términos de entalpía :
dH = dQ + Vdp
o
dH = TdS + Vdp
Proceso isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1
Proceso isobárico
Un proceso isobárico es un proceso termodinámico , en el cual la presión del sistema permanece constante (p = const). La transferencia de calor dentro o fuera del sistema funciona, pero también cambia la energía interna del sistema.
Dado que hay cambios en la energía interna (dU) y cambios en el volumen del sistema (∆V), los ingenieros a menudo usan la entalpía del sistema, que se define como:
H = U + pV
Proceso isobárico y la primera ley
La forma clásica de la primera ley de la termodinámica es la siguiente ecuación:
dU = dQ – dW
En esta ecuación, dW es igual a dW = pdV y se conoce como el trabajo límite . En un proceso isobárico y el gas ideal, parte del calor agregado al sistema se utilizará para hacer el trabajo y parte del calor agregado aumentará la energía interna (aumentará la temperatura). Por lo tanto, es conveniente utilizar la entalpía en lugar de la energía interna.
Proceso isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
En una entropía constante , es decir, en un proceso isentrópico, el cambio de entalpía es igual al trabajo del proceso de flujo realizado en o por el sistema.
Ciclo de Rankine – pV, diagrama Ts
El ciclo de Rankine a menudo se representa en un diagrama de volumen de presión (diagrama pV ) y en un diagrama de temperatura-entropía ( diagrama Ts ).
Cuando se trazan en un diagrama de volumen de presión , los procesos isobáricos siguen las líneas isobáricas para el gas (las líneas horizontales), los procesos adiabáticos se mueven entre estas líneas horizontales y el área delimitada por la ruta completa del ciclo representa el trabajo total que se puede hacer durante uno ciclo.
El diagrama de temperatura-entropía ( diagrama Ts) en el que el estado termodinámico se especifica mediante un punto en un gráfico con entropía específica (s) como eje horizontal y temperatura absoluta (T) como eje vertical. Los diagramas Ts son una herramienta útil y común, particularmente porque ayuda a visualizar la transferencia de calor durante un proceso. Para procesos reversibles (ideales), el área bajo la curva Ts de un proceso es el calor transferido al sistema durante ese proceso.
Eficiencia térmica del ciclo de Rankine
En general, la eficiencia térmica , η º , de cualquier motor de calor se define como la relación de la obra lo hace, W , para el calor de entrada a la alta temperatura, Q H .
La eficiencia térmica , η th , representa la fracción de calor , Q H , que se convierte en trabajo . Dado que la energía se conserva de acuerdo con la primera ley de la termodinámica y la energía no se puede convertir para trabajar por completo, la entrada de calor, Q H , debe ser igual al trabajo realizado, W, más el calor que se debe disipar como calor residual Q C en el ambiente. Por lo tanto, podemos reescribir la fórmula para la eficiencia térmica como:
Esta es una fórmula muy útil, pero aquí expresamos la eficiencia térmica utilizando la primera ley en términos de entalpía .
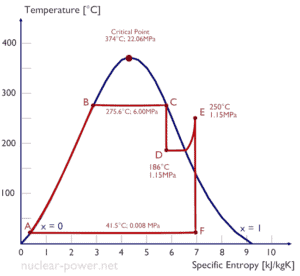
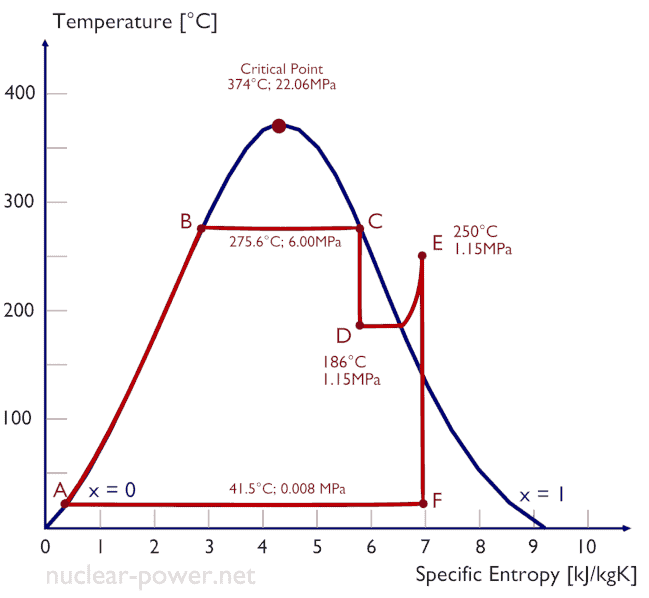
Típicamente, la mayoría de las centrales nucleares opera turbinas de vapor de condensación de etapas múltiples . En estas turbinas, la etapa de alta presión recibe vapor (este vapor es vapor casi saturado – x = 0.995 – punto C en la figura; 6 MPa ; 275.6 ° C) desde un generador de vapor y lo expulsa al separador-recalentador de humedad (punto D ) El vapor debe recalentarse para evitar daños que puedan ocasionar a las aspas de la turbina de vapor el vapor de baja calidad . El recalentador calienta el vapor (punto D) y luego el vapor se dirige a la etapa de baja presión de la turbina de vapor, donde se expande (punto E a F). El vapor agotado se condensa en el condensador y está a una presión muy por debajo de la atmosférica (presión absoluta de0.008 MPa ), y está en un estado parcialmente condensado (punto F), típicamente de una calidad cercana al 90%.
En este caso, los generadores de vapor, la turbina de vapor, los condensadores y las bombas de agua de alimentación constituyen un motor térmico, sujeto a las limitaciones de eficiencia impuestas por la segunda ley de la termodinámica . En el caso ideal (sin fricción, procesos reversibles, diseño perfecto), este motor térmico tendría una eficiencia de Carnot de
= 1 – T frío / T caliente = 1 – 315/549 = 42.6%
donde la temperatura del depósito caliente es 275.6 ° C (548.7K), la temperatura del depósito frío es 41.5 ° C (314.7K). Pero la central nuclear es el motor térmico real , en el que los procesos termodinámicos son de alguna manera irreversibles. No se hacen infinitamente lento. En dispositivos reales (como turbinas, bombas y compresores) una fricción mecánica y pérdidas de calor causan pérdidas adicionales de eficiencia.
Para calcular la eficiencia térmica del ciclo de Rankine más simple (sin recalentamiento), los ingenieros utilizan la primera ley de la termodinámica en términos de entalpía en lugar de en términos de energía interna.
La primera ley en términos de entalpía es:
dH = dQ + Vdp
En esta ecuación, el término Vdp es un proceso de flujo de trabajo. Este trabajo, Vdp , se utiliza para sistemas de flujo abierto como una turbina o una bomba en la que hay un “dp” , es decir, un cambio de presión. No hay cambios en el volumen de control . Como puede verse, esta forma de ley simplifica la descripción de la transferencia de energía . A presión constante , el cambio de entalpía es igual a la energía transferida del ambiente a través del calentamiento:
Proceso isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
En una entropía constante , es decir, en un proceso isentrópico, el cambio de entalpía es igual al trabajo del proceso de flujo realizado en o por el sistema:
Proceso isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1
Es obvio, será muy útil en el análisis de los dos ciclos termodinámicos utilizados en la ingeniería de energía, es decir, en el ciclo de Brayton y el ciclo de Rankine.
La entalpía se puede convertir en una variable intensiva o específica dividiéndola por la masa . Los ingenieros usan la entalpía específica en el análisis termodinámico más que la entalpía misma. Se tabula en las tablas de vapor junto con un volumen específico y una energía interna específica . La eficiencia térmica de dicho ciclo simple de Rankine y en términos de entalpías específicas sería:
Es una ecuación muy simple y para determinar la eficiencia térmica puede usar datos de tablas de vapor .
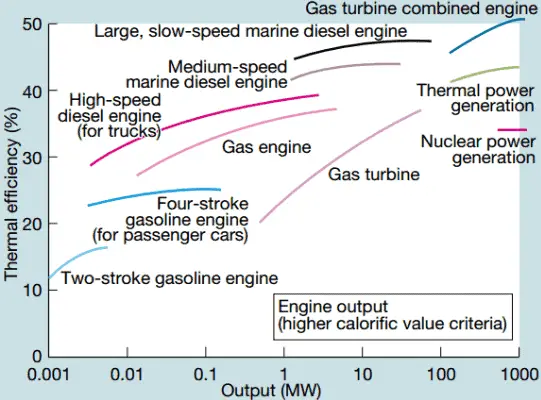
En las centrales nucleares modernas, la eficiencia térmica general es de aproximadamente un tercio (33%), por lo que se necesitan 3000 MWth de energía térmica de la reacción de fisión para generar 1000 MWe de energía eléctrica. La razón radica en una temperatura de vapor relativamente baja ( 6 MPa ; 275.6 ° C). Se pueden lograr mayores eficiencias aumentando la temperaturadel vapor Pero esto requiere un aumento de las presiones dentro de las calderas o generadores de vapor. Sin embargo, las consideraciones metalúrgicas ponen límites superiores a tales presiones. En comparación con otras fuentes de energía, la eficiencia térmica del 33% no es mucho. Pero debe tenerse en cuenta que las centrales nucleares son mucho más complejas que las centrales de combustibles fósiles y es mucho más fácil quemar combustibles fósiles que generar energía a partir de combustibles nucleares. Las plantas de energía de combustible fósil subcrítico, que funcionan bajo presión crítica (es decir, por debajo de 22.1 MPa), pueden lograr una eficiencia de 36 a 40%.
Mejora de la eficiencia térmica – Ciclo Rankine
Existen varios métodos, ¿cómo puede mejorar la eficiencia térmica del ciclo de Rankine? Suponiendo que la temperatura máxima está limitada por la presión dentro del recipiente a presión del reactor, estos métodos son:
- Presiones de caldera y condensador
- Sobrecalentamiento y recalentamiento
- Regeneración de calor
- Ciclo supercrítico de Rankine
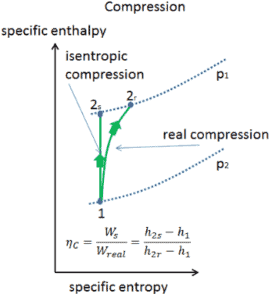
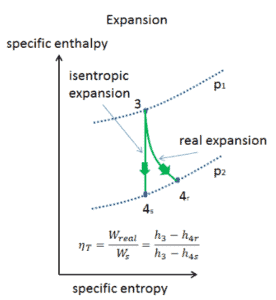
Eficiencia isentrópica: turbina, bomba
En capítulos anteriores supusimos que la expansión del vapor es isentrópica y, por lo tanto, usamos T 4, como la temperatura de salida del gas. Estos supuestos solo son aplicables con ciclos ideales.
La mayoría de los dispositivos de flujo constante (turbinas, compresores, boquillas) funcionan en condiciones adiabáticas, pero no son realmente isentrópicos, sino que están idealizados como isentrópicos para fines de cálculo. Definimos los parámetros η T , η P , η N , como una relación entre el trabajo real realizado por el dispositivo y el trabajo del dispositivo cuando se opera en condiciones isentrópicas (en el caso de una turbina). Esta relación se conoce como la eficiencia de la turbina isentrópica / bomba / boquilla . Estos parámetros describen qué tan eficientemente una turbina, compresor o boquilla se aproxima a un dispositivo isentrópico correspondiente. Este parámetro reduce la eficiencia general y el rendimiento del trabajo. Para turbinas, el valor de η T es típicamente de 0.7 a 0.9 (70-90%).
Ver también: proceso isentrópico
Turbina de vapor: problema con la solución
Supongamos el ciclo de Rankine , que es uno de los ciclos termodinámicos más comunes en las centrales térmicas. En este caso, suponga un ciclo simple sin recalentamiento y sin turbina de vapor de condensación funcionando con vapor saturado (vapor seco). En este caso, la turbina opera en estado estable con condiciones de entrada de 6 MPa, t = 275.6 ° C, x = 1 (punto 3). El vapor sale de esta etapa de la turbina a una presión de 0.008 MPa, 41.5 ° C yx = ??? (punto 4).
Calcular:
- la calidad del vapor del vapor de salida
- la diferencia de entalpía entre estos dos estados (3 → 4), que corresponde al trabajo realizado por el vapor, W T .
- la diferencia de entalpía entre estos dos estados (1 → 2), que corresponde a la labor realizada por las bombas, W P .
- La diferencia de entalpía entre estos dos estados (2 → 3), que corresponde al calor neto agregado en el generador de vapor
- la eficiencia termodinámica de este ciclo y compare este valor con la eficiencia de Carnot
1)
Como no conocemos la calidad exacta del vapor del vapor de salida, tenemos que determinar este parámetro. El estado 4 está fijado por la presión p 4 = 0.008 MPa y el hecho de que la entropía específica es constante para la expansión isentrópica (s 3 = s 4 = 5.89 kJ / kgK para 6 MPa ). La entropía específica del agua líquida saturada (x = 0) y el vapor seco (x = 1) puede seleccionarse de las tablas de vapor . En caso de vapor húmedo, la entropía real se puede calcular con la calidad del vapor, x, y las entropías específicas de agua líquida saturada y vapor seco:
s 4 = s v x + (1 – x) s l
dónde
s 4 = entropía de vapor húmedo (J / kg K) = 5.89 kJ / kgK
s v = entropía de vapor “seco” (J / kg K) = 8.227 kJ / kgK (para 0.008 MPa)
s l = entropía de agua líquida saturada (J / kg K) = 0.592 kJ / kgK (para 0.008 MPa)
De esta ecuación, la calidad del vapor es:
x 4 = ( s 4 – s l ) / ( s v – s l ) = (5.89 – 0.592) / (8.227 – 0.592) = 0.694 = 69.4%
2)
La entalpía para el estado 3 puede seleccionarse directamente de las mesas de vapor, mientras que la entalpía para el estado 4 debe calcularse utilizando la calidad del vapor:
h 3, v = 2785 kJ / kg
h 4, húmedo = h 4, v x + (1 – x) h 4, l = 2576. 0.694 + (1 – 0.694). 174 = 1787 + 53,2 = 1840 kJ / kg
Entonces el trabajo realizado por el vapor, W T, es
W T = Δh = 945 kJ / kg
3)
La entalpía para el estado 1 puede seleccionarse directamente de las mesas de vapor:
h 1, l = 174 kJ / kg
El estado 2 está fijado por la presión p 2 = 6.0 MPa y el hecho de que la entropía específica es constante para la compresión isentrópica (s 1 = s 2 = 0.592 kJ / kgK para 0.008 MPa ). Para esta entropía s 2 = 0.592 kJ / kgK y p 2 = 6.0 MPa encontramos h 2, subenfriado en tablas de vapor para agua comprimida (usando interpolación entre dos estados).
h 2, subenfriado = 179.7 kJ / kg
Entonces el trabajo realizado por las bombas, W P, es
W P = Δh = 5.7 kJ / kg
4)
La diferencia de entalpía entre (2 → 3), que corresponde al calor neto agregado en el generador de vapor, es simplemente:
Q add = h 3, v – h 2, subenfriado = 2785 – 179.7 = 2605.3 kJ / kg
Tenga en cuenta que no hay regeneración de calor en este ciclo. Por otro lado, la mayor parte del calor agregado es para la entalpía de vaporización (es decir, para el cambio de fase).
5)
En este caso, los generadores de vapor, la turbina de vapor, los condensadores y las bombas de agua de alimentación constituyen un motor térmico, sujeto a las limitaciones de eficiencia impuestas por la segunda ley de la termodinámica . En el caso ideal (sin fricción, procesos reversibles, diseño perfecto), este motor térmico tendría una eficiencia de Carnot de
η Carnot = 1 – T frío / T caliente = 1 – 315/549 = 42.6%
donde la temperatura del depósito caliente es de 275.6 ° C (548.7 K), la temperatura del depósito frío es de 41.5 ° C (314.7K).
La eficiencia termodinámica de este ciclo se puede calcular mediante la siguiente fórmula:
así
η th = (945 – 5.7) / 2605.3 = 0.361 = 36.1%
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.
