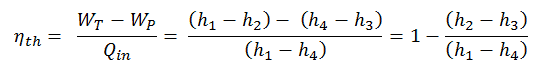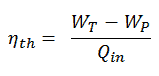Theorie der Dampfturbinen – Thermodynamik
1859 brachte der schottische Ingenieur William John Macquorn Rankine das Studium der Wärmekraftmaschinen voran, indem er das „ Handbuch der Dampfmaschine und anderer Hauptantriebe “ veröffentlichte. Rankine entwickelte eine vollständige Theorie der Dampfmaschine und aller Wärmekraftmaschinen. Zusammen mit Rudolf Clausius und William Thomson (Lord Kelvin) leistete er einen Beitrag zur Thermodynamik, wobei er sich insbesondere auf das erste der drei thermodynamischen Gesetze konzentrierte.
Der Rankine-Zyklus wurde nach ihm benannt und beschreibt die Leistung von Dampfturbinensystemen , obwohl das theoretische Prinzip auch für Hubkolbenmotoren wie Dampflokomotiven gilt. Im Allgemeinen ist der Rankine-Zyklus ein idealisierter thermodynamischer Zyklus einer Wärmekraftmaschine mit konstantem Druck, der einen Teil der Wärme in mechanische Arbeit umwandelt. In diesem Zyklus wird die Wärme extern einem geschlossenen Kreislauf zugeführt, der normalerweise Wasser (in flüssiger und dampfförmiger Phase) als Arbeitsmedium verwendet. Im Gegensatz zu dem Zyklus Brayton , das Fluid in dem Arbeits Rankine – Zyklus durchläuft die Phasenänderung von einer Flüssigkeit in Dampfphase und vice versa.
Während viele Substanzen als Arbeitsfluid im Rankine-Kreislauf verwendet werden könnten (anorganisch oder sogar organisch), ist Wasser aufgrund seiner günstigen Eigenschaften, wie seiner ungiftigen und nicht reaktiven Chemie, seiner Häufigkeit und seiner geringen Kosten, normalerweise das Fluid der Wahl. sowie seine thermodynamischen Eigenschaften. Zum Beispiel hat Wasser die höchste spezifische Wärme aller gängigen Substanzen – 4,19 kJ / kg K. Darüber hinaus hat es eine sehr hohe Verdampfungswärme , was es zu einem wirksamen Kühlmittel und Medium in Wärmekraftwerken und anderen Energiebranchen macht. Im Falle des Rankine-Zyklus das ideale Gasgesetzkann fast nicht verwendet werden (Dampf folgt nicht pV = nRT), daher sind alle wichtigen Parameter von Wasser und Dampf in sogenannten „ Dampftabellen “ aufgeführt.
Einer der Hauptvorteile des Rankine-Zyklus besteht darin, dass der Kompressionsprozess in der Pumpe an einer Flüssigkeit stattfindet . Durch Kondensieren des Arbeitsdampfes zu einer Flüssigkeit (innerhalb eines Kondensators) wird der Druck am Turbinenausgang gesenkt und die von der Förderpumpe benötigte Energie verbraucht nur 1% bis 3% der Turbinenausgangsleistung und diese Faktoren tragen zu einem höheren Wirkungsgrad bei der Kreislauf.
Der Rankine-Kreislauf ist heute der grundlegende Betriebszyklus aller Wärmekraftwerke, in denen ein Betriebsfluid kontinuierlich verdampft und kondensiert. Dies ist einer der häufigsten thermodynamischen Kreisprozessen, da die Turbine an den meisten Orten der Welt mit Dampf angetrieben wird.
Im Gegensatz zum Carnot-Zyklus führt der Rankine-Zyklus keine isothermen Prozesse aus, da diese sehr langsam ausgeführt werden müssen. In einem idealen Rankine-Zyklus durchläuft das System, das den Zyklus ausführt, eine Reihe von vier Prozessen: zwei isentrope (reversible adiabatische) Prozesse, die sich mit zwei isobaren Prozessen abwechseln.
Da das Carnot-Prinzip besagt, dass kein Motor effizienter sein kann als ein reversibler Motor ( eine Carnot-Wärmekraftmaschine ), der zwischen denselben Hochtemperatur- und Niedertemperaturspeichern betrieben wird, muss eine auf dem Rankine-Zyklus basierende Dampfturbine einen geringeren Wirkungsgrad aufweisen als der Carnot-Wirkungsgrad.
In modernen Kernkraftwerken beträgt der thermische Gesamtwirkungsgrad etwa ein Drittel (33%), sodass 3000 MWth Wärmeleistung aus der Spaltreaktion benötigt werden, um 1000 MWe elektrischen Strom zu erzeugen . Höhere Wirkungsgrade können durch Erhöhen der Temperatur des Dampfes erreicht werden . Dies erfordert jedoch einen Druckanstieg in Kesseln oder Dampferzeugern. Metallurgische Überlegungen begrenzen solche Drücke jedoch. Im Vergleich zu anderen Energiequellen ist der thermische Wirkungsgrad von 33% nicht viel. Es ist jedoch zu beachten, dass Kernkraftwerke viel komplexer sind als Kraftwerke mit fossilen Brennstoffen und es viel einfacher ist, fossile Brennstoffe zu verbrennen, als Energie aus Kernbrennstoffen zu erzeugen .
Rankine-Zyklus – Prozesse
In einem idealen Rankine-Zyklus durchläuft das System, das den Zyklus ausführt, eine Reihe von vier Prozessen: zwei isentrope (reversible adiabatische) Prozesse, die sich mit zwei isobaren Prozessen abwechseln:
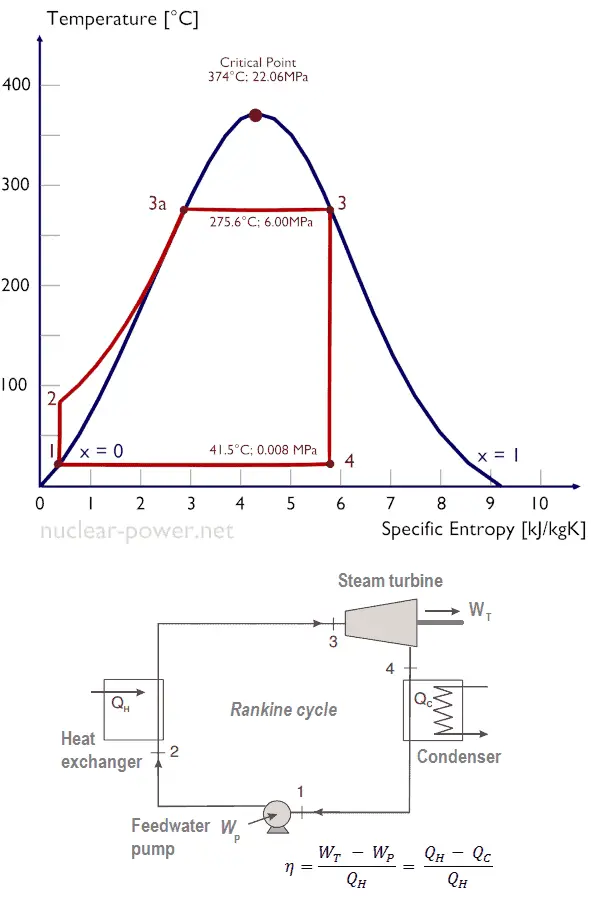 Isentropische Kompression (Kompression in Kreiselpumpen) – Das flüssige Kondensat wird durch Kreiselpumpen (normalerweise durch Kondensatpumpen und dann durch Speisewasserpumpen) adiabatisch von Zustand 1 auf Zustand 2 komprimiert. Das flüssige Kondensat wird vom Kondensator in den Hochdruckkessel gepumpt. In diesem Prozess arbeitet die Umgebung an der Flüssigkeit, erhöht ihre Enthalpie (h = u + pv) und komprimiert sie (erhöht ihren Druck). Andererseits bleibt die Entropie unverändert. Die für den Kompressor erforderliche Arbeit ergibt sich aus W Pumpen = H 2 – H 1 .
Isentropische Kompression (Kompression in Kreiselpumpen) – Das flüssige Kondensat wird durch Kreiselpumpen (normalerweise durch Kondensatpumpen und dann durch Speisewasserpumpen) adiabatisch von Zustand 1 auf Zustand 2 komprimiert. Das flüssige Kondensat wird vom Kondensator in den Hochdruckkessel gepumpt. In diesem Prozess arbeitet die Umgebung an der Flüssigkeit, erhöht ihre Enthalpie (h = u + pv) und komprimiert sie (erhöht ihren Druck). Andererseits bleibt die Entropie unverändert. Die für den Kompressor erforderliche Arbeit ergibt sich aus W Pumpen = H 2 – H 1 .- Isobare Wärmezufuhr (in einem Wärmetauscher – Kessel) – In dieser Phase (zwischen Zustand 2 und Zustand 3) erfolgt eine Wärmeübertragung mit konstantem Druck von einer externen Quelle auf das flüssige Kondensat, da die Kammer zum Ein- und Ausströmen geöffnet ist . Das Speisewasser (Sekundärkreislauf) wird vom Siedepunkt (2 → 3a) dieser Flüssigkeit erwärmt und dann im Kessel (3a → 3) verdampft. Die hinzugefügte Nettowärme ist gegeben durch Q add = H 3 – H 2
- Isentropische Expansion (Expansion in einer Dampfturbine) – Dampf aus dem Kessel expandiert adiabatisch von Zustand 3 zu Zustand 4 in einer Dampfturbine, um Arbeit zu erzeugen, und wird dann in den Kondensator abgegeben (teilweise kondensiert). Der Dampf wirkt auf die Umgebung (Schaufeln der Turbine) und verliert eine Enthalpie, die der Arbeit entspricht, die das System verlässt. Die von der Turbine geleistete Arbeit ist gegeben durch W T = H 4 – H 3 . Auch hier bleibt die Entropie unverändert.
- Isobare Wärmeabgabe (in einem Wärmetauscher) – In dieser Phase wird der Zyklus durch einen Prozess mit konstantem Druck abgeschlossen, bei dem Wärme aus dem teilweise kondensierten Dampf abgegeben wird. In einem Kühlkreislauf fließt Wärme vom Dampf auf das Kühlwasser. Der Dampf kondensiert und die Temperatur des Kühlwassers steigt an. Die abgegebene Nettowärme ist gegeben durch Q re = H 4 – H 1
Während eines Rankine-Zyklus wird von den Pumpen zwischen den Zuständen 1 und 2 ( i sentropische Kompression ) an der Flüssigkeit gearbeitet . Die Arbeit wird von der Flüssigkeit in der Turbine zwischen den Stufen 3 und 4 ausgeführt ( i sentropische Expansion ). Der Unterschied zwischen der von der Flüssigkeit geleisteten Arbeit und der an der Flüssigkeit geleisteten Arbeit ist die vom Zyklus erzeugte Netzarbeit und entspricht der von der Zykluskurve eingeschlossenen Fläche (im pV-Diagramm). Das Arbeitsfluid in einem Rankine-Zyklus folgt einem geschlossenen Kreislauf und wird ständig wiederverwendet.
Wie zu sehen ist, ist es zweckmäßig, bei der Analyse dieses thermodynamischen Zyklus die Enthalpie und das erste Gesetz in Bezug auf die Enthalpie zu verwenden. Diese Form des Gesetzes vereinfacht die Beschreibung der Energieübertragung . Bei konstantem Druck entspricht die Enthalpieänderung der Energie , die durch Erhitzen aus der Umgebung übertragen wird:
Isobarer Prozess (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Bei konstanter Entropie , dh im isentropischen Prozess, entspricht die Enthalpieänderung der am oder vom System durchgeführten Flussprozessarbeit :
Isentropischer Prozess (dQ = 0):
dH = Vdp → W = H 2 – H 1
Siehe auch: Warum verwenden Energieingenieure Enthalpie? Antwort: dH = dQ + Vdp
Isentropischer Prozess
Ein isentropischer Prozess ist ein thermodynamischer Prozess , bei dem die Entropie des Fluids oder Gases konstant bleibt. Dies bedeutet, dass der isentrope Prozess ein Sonderfall eines adiabatischen Prozesses ist, bei dem keine Wärme- oder Materieübertragung stattfindet. Es ist ein reversibler adiabatischer Prozess . Die Annahme, dass keine Wärmeübertragung stattfindet, ist sehr wichtig, da wir die adiabatische Näherung nur in sehr schnellen Prozessen verwenden können .
Isentropischer Prozess und das erste Gesetz
Für ein geschlossenes System können wir den ersten Hauptsatz der Thermodynamik in Bezug auf die Enthalpie schreiben :
dH = dQ + Vdp
oder
dH = TdS + Vdp
Isentropischer Prozess (dQ = 0):
dH = Vdp → W = H 2 – H 1
Isobarer Prozess
Ein isobarer Prozess ist ein thermodynamischer Prozess , bei dem der Druck des Systems konstant bleibt (p = const). Die Wärmeübertragung in oder aus dem System funktioniert zwar, verändert aber auch die innere Energie des Systems.
Da sich die innere Energie (dU) und das Systemvolumen (∆V) ändern, verwenden Ingenieure häufig die Enthalpie des Systems, die wie folgt definiert ist:
H = U + pV
Isobarer Prozess und das erste Gesetz
Die klassische Form des ersten Hauptsatzes der Thermodynamik ist die folgende Gleichung:
dU = dQ – dW
In dieser Gleichung ist dW gleich dW = pdV und ist bekannt als die Grenz Arbeit . Bei einem isobaren Prozess und dem idealen Gas wird ein Teil der dem System zugeführten Wärme für die Arbeit verwendet, und ein Teil der zugeführten Wärme erhöht die innere Energie (erhöht die Temperatur). Daher ist es zweckmäßig, die Enthalpie anstelle der inneren Energie zu verwenden.
Isobarer Prozess (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Bei konstanter Entropie , dh im isentropischen Prozess, entspricht die Enthalpieänderung der Flussprozessarbeit, die am oder vom System ausgeführt wird.
Rankine-Zyklus – pV, Ts-Diagramm
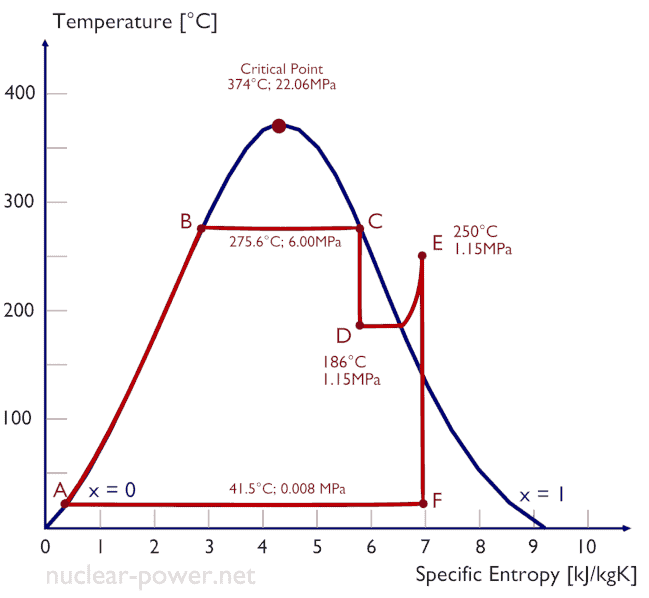
Der Rankine-Zyklus wird häufig in einem Druckvolumendiagramm ( pV-Diagramm ) und in einem Temperatur-Entropie-Diagramm ( Ts-Diagramm ) aufgezeichnet .
Wenn sie auf einem aufgetragen P-V-Diagramm , die isobare Verfahren der isobare Leitungen für das Gas (die horizontalen Linien) folgen, adiabatische Prozesse zwischen diesen horizontalen Linien bewegen , und die durch den gesamten Zyklus hinweg Pfad begrenzt Bereich stellt die gesamte Arbeit , die während einem getan werden kann , Zyklus.
Das Temperatur-Entropie-Diagramm (Ts-Diagramm), in dem der thermodynamische Zustand durch einen Punkt in einem Diagramm mit spezifischen Entropien als horizontale Achse und absoluter Temperatur (T) als vertikaler Achse angegeben wird. Ts-Diagramme sind ein nützliches und allgemeines Werkzeug, insbesondere weil sie dazu beitragen, die Wärmeübertragung während eines Prozesses zu visualisieren . Bei reversiblen (idealen) Prozessen ist die Fläche unter der Ts-Kurve eines Prozesses die Wärme , die während dieses Prozesses auf das System übertragen wird.
Thermische Effizienz des Rankine-Zyklus
Im allgemeinen wird die thermischen Wirkungsgrad , η th , ein Wärmekraftmaschine ist als das Verhältnis der definierten Arbeits es tut, W , an den Wärmeeingang bei der hohen Temperatur, Q H .
Der thermische Wirkungsgrad , η th , stellt den Anteil an Wärme , Q H , die konvertiert wird , zu arbeiten . Da Energie nach dem ersten Hauptsatz der Thermodynamik eingespart wird und Energie nicht vollständig in Arbeit umgewandelt werden kann , muss der Wärmeeintrag Q H gleich der geleisteten Arbeit W plus der Wärme sein, die als Abwärme Q C an die abgegeben werden muss Umgebung. Daher können wir die Formel für den thermischen Wirkungsgrad wie folgt umschreiben:
Dies ist eine sehr nützliche Formel, aber hier drücken wir den thermischen Wirkungsgrad unter Verwendung des ersten Gesetzes in Bezug auf die Enthalpie aus .
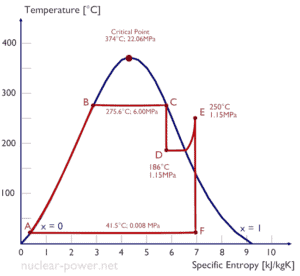
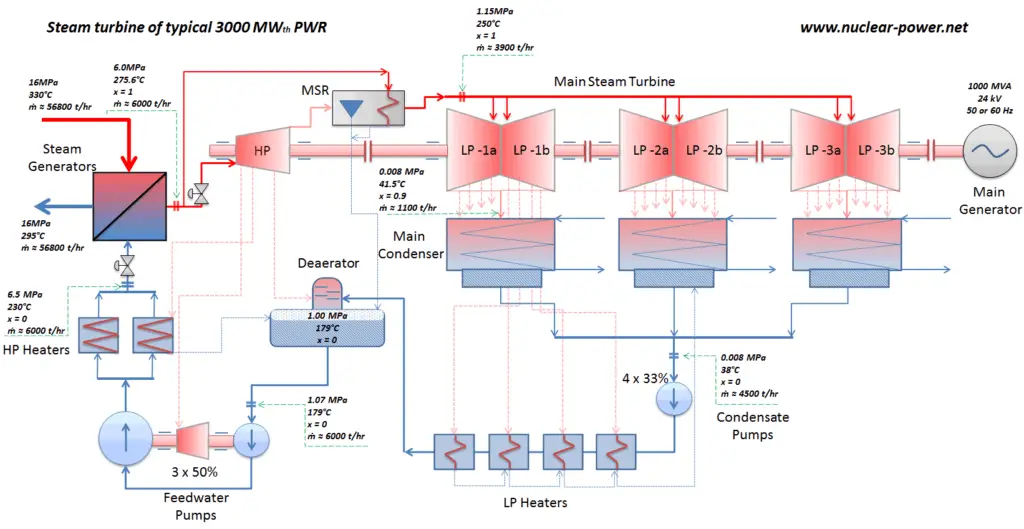
Typischerweise betreiben die meisten Kernkraftwerke mehrstufige Kondensationsdampfturbinen . In diesen Turbinen erhält die Hochdruckstufe Dampf (dieser Dampf ist nahezu gesättigter Dampf – x = 0,995 – Punkt C in der Abbildung; 6 MPa ; 275,6 ° C) von einem Dampferzeuger und leitet ihn zum Feuchtigkeitsabscheider-Nacherhitzer (Punkt D) ab ). Der Dampf muss erneut erwärmt werden, um Schäden zu vermeiden, die durch Dampf von geringer Qualität an den Schaufeln der Dampfturbine verursacht werden könnten . Der Nacherhitzer erwärmt den Dampf (Punkt D) und dann wird der Dampf zur Niederdruckstufe der Dampfturbine geleitet, wo er sich ausdehnt (Punkt E bis F). Der ausgestoßene Dampf kondensiert dann im Kondensator und hat einen Druck, der weit unter dem atmosphärischen Druck (absoluter Druck von0,008 MPa ) und befindet sich in einem teilweise kondensierten Zustand (Punkt F), typischerweise von einer Qualität nahe 90%.
In diesem Fall bilden Dampferzeuger, Dampfturbinen, Kondensatoren und Speisewasserpumpen eine Wärmekraftmaschine, die den durch den zweiten Hauptsatz der Thermodynamik auferlegten Effizienzbeschränkungen unterliegt . Im Idealfall (keine Reibung, reversible Prozesse, perfektes Design) hätte diese Wärmekraftmaschine einen Carnot-Wirkungsgrad von
= 1 – T kalt / T heiß = 1 – 315/549 = 42,6%
Wenn die Temperatur des heißen Reservoirs 275,6 ° C (548,7 K) beträgt, beträgt die Temperatur des kalten Reservoirs 41,5 ° C (314,7 K). Das Kernkraftwerk ist jedoch die eigentliche Wärmekraftmaschine , in der thermodynamische Prozesse irgendwie irreversibel sind. Sie werden nicht unendlich langsam gemacht. In realen Geräten (wie Turbinen, Pumpen und Kompressoren) verursachen mechanische Reibung und Wärmeverluste weitere Wirkungsgradverluste.
Um den thermischen Wirkungsgrad des einfachsten Rankine-Zyklus (ohne Wiedererwärmung) zu berechnen, verwenden Ingenieure den ersten Hauptsatz der Thermodynamik eher in Bezug auf die Enthalpie als in Bezug auf die innere Energie.
Das erste Gesetz in Bezug auf die Enthalpie lautet:
dH = dQ + Vdp
In dieser Gleichung ist der Begriff Vdp eine Flussprozessarbeit. Diese Arbeit, Vdp , wird für Open-Flow-Systeme wie eine Turbine oder eine Pumpe verwendet, bei denen ein „dp“ vorliegt , dh eine Druckänderung. Es gibt keine Änderungen in der Lautstärke . Wie zu sehen ist, vereinfacht diese Form des Gesetzes die Beschreibung der Energieübertragung . Bei konstantem Druck entspricht die Enthalpieänderung der Energie , die durch Erhitzen aus der Umgebung übertragen wird:
Isobarer Prozess (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Bei konstanter Entropie , dh im isentropischen Prozess, entspricht die Enthalpieänderung der am oder vom System durchgeführten Flussprozessarbeit :
Isentropischer Prozess (dQ = 0):
dH = Vdp → W = H 2 – H 1
Es ist offensichtlich, dass es bei der Analyse sowohl der in der Energietechnik verwendeten thermodynamischen Kreisprozessen, dh des Brayton-Zyklus als auch des Rankine-Zyklus, sehr nützlich sein wird.
Die Enthalpie kann durch Teilen durch die Masse zu einer intensiven oder spezifischen Variablen gemacht werden . Ingenieure verwenden die spezifische Enthalpie in der thermodynamischen Analyse mehr als die Enthalpie selbst. Es ist in den Dampftabellen zusammen mit dem spezifischen Volumen und der spezifischen inneren Energie aufgeführt . Der thermische Wirkungsgrad eines solchen einfachen Rankine-Zyklus und in Bezug auf spezifische Enthalpien wäre:
Es ist eine sehr einfache Gleichung und zur Bestimmung des thermischen Wirkungsgrads können Sie Daten aus Dampftabellen verwenden .
In modernen Kernkraftwerken beträgt der thermische Gesamtwirkungsgrad etwa ein Drittel (33%), sodass 3000 MWth Wärmeleistung aus der Spaltreaktion benötigt werden, um 1000 MWe elektrischen Strom zu erzeugen . Der Grund liegt in der relativ niedrigen Dampftemperatur ( 6 MPa ; 275,6 ° C). Höhere Wirkungsgrade können durch Erhöhen der Temperatur erreicht werdendes Dampfes. Dies erfordert jedoch einen Druckanstieg in Kesseln oder Dampferzeugern. Metallurgische Überlegungen begrenzen solche Drücke jedoch. Im Vergleich zu anderen Energiequellen ist der thermische Wirkungsgrad von 33% nicht viel. Es ist jedoch zu beachten, dass Kernkraftwerke viel komplexer sind als Kraftwerke mit fossilen Brennstoffen und es viel einfacher ist, fossile Brennstoffe zu verbrennen, als Energie aus Kernbrennstoffen zu erzeugen. Unterkritische Kraftwerke mit fossilen Brennstoffen, die unter kritischem Druck (dh unter 22,1 MPa) betrieben werden, können einen Wirkungsgrad von 36–40% erreichen.
Ursachen für Ineffizienz
Wie bereits erwähnt, kann ein Wirkungsgrad zwischen 0 und 1 liegen. Jede Wärmekraftmaschine ist irgendwie ineffizient. Diese Ineffizienz kann auf drei Ursachen zurückgeführt werden.
- Irreversibilität von Prozessen . Es gibt eine theoretische Obergrenze für die Effizienz der Umwandlung von Wärme in Arbeit in jeder Wärmekraftmaschine. Diese Obergrenze wird als Carnot-Effizienz bezeichnet . Nach dem Carnot-Prinzip kann kein Motor effizienter sein als ein reversibler Motor ( eine Carnot-Wärmekraftmaschine ), der zwischen denselben Hochtemperatur- und Niedertemperaturbehältern arbeitet. Wenn beispielsweise der heiße Vorratsbehälter T heiß von 400 ° C (673 K) und T kalt von etwa 20 ° C (293 K) aufweist, beträgt der maximale (ideale) Wirkungsgrad: = 1 – T kalt / T heiß = 1 – 293 / 673 = 56%. Aber alle realen thermodynamischen Prozesse sind irgendwie irreversibel. Sie werden nicht unendlich langsam gemacht. Daher müssen Wärmekraftmaschinen aufgrund der inhärenten Irreversibilität des von ihnen verwendeten Wärmekraftmaschinenzyklus niedrigere Wirkungsgrade als Grenzwerte für ihren Wirkungsgrad aufweisen.
- Vorhandensein von Reibung und Wärmeverlusten. In realen thermodynamischen Systemen oder in realen Wärmekraftmaschinen ist ein Teil der Ineffizienz des Gesamtzyklus auf die Verluste der einzelnen Komponenten zurückzuführen. In realen Geräten (wie Turbinen, Pumpen und Kompressoren) verursachen mechanische Reibung , Wärmeverluste und Verluste im Verbrennungsprozess weitere Effizienzverluste.
- Design-Ineffizienz . Die letzte und auch wichtige Ursache für Ineffizienzen sind die Kompromisse, die Ingenieure bei der Konstruktion einer Wärmekraftmaschine (z. B. eines Kraftwerks) eingegangen sind. Sie müssen Kosten und andere Faktoren bei der Auslegung und dem Betrieb des Zyklus berücksichtigen. Betrachten Sie als Beispiel eine Auslegung des Kondensators in den Wärmekraftwerken. Idealerweise würde der in den Kondensator abgegebene Dampf keine Unterkühlung aufweisen . Echte Kondensatoren sind jedoch so ausgelegt, dass sie die Flüssigkeit um einige Grad Celsius unterkühlen, um die Saugkavitation in den Kondensatpumpen zu vermeiden . Diese Unterkühlung erhöht jedoch die Ineffizienz des Kreislaufs, da mehr Energie zum Wiedererhitzen des Wassers benötigt wird.
Verbesserung der thermischen Effizienz – Rankine-Zyklus
Es gibt verschiedene Methoden, wie der thermische Wirkungsgrad des Rankine-Zyklus verbessert werden kann. Unter der Annahme, dass die maximale Temperatur durch den Druck im Reaktordruckbehälter begrenzt ist, sind diese Methoden:
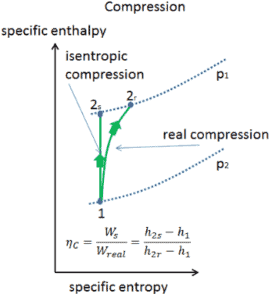
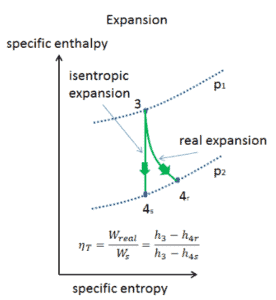
Isentrope Effizienz – Turbine, Pumpe
In den vorhergehenden Kapiteln haben wir angenommen, dass die Dampfexpansion isentrop ist, und deshalb haben wir T 4 als Austrittstemperatur des Gases verwendet. Diese Annahmen gelten nur für ideale Kreisprozessen.
Die meisten Steady-Flow-Geräte (Turbinen, Kompressoren, Düsen) arbeiten unter adiabatischen Bedingungen, sind jedoch nicht wirklich isentrop, sondern für Berechnungszwecke eher als isentrop idealisiert. Wir definieren Parameter η T , η P , η N , als Verhältnis der eigentlichen Arbeit durch die Vorrichtung zu arbeiten , indem Gerät durchgeführt , wenn sie unter Bedingungen isentroper (im Fall von Turbinen) betrieben. Dieses Verhältnis ist als Effizienz der isentropischen Turbine / Pumpe / Düse bekannt . Diese Parameter beschreiben, wie effizient sich eine Turbine, ein Kompressor oder eine Düse einer entsprechenden isentropischen Vorrichtung annähert. Dieser Parameter reduziert die Gesamteffizienz und die Arbeitsleistung. Für Turbinen beträgt der Wert von η T typischerweise 0,7 bis 0,9 (70–90%).
Siehe auch: Isentropischer Prozess
Dampfturbine – Problem mit der Lösung
 Nehmen wir den Rankine-Zyklus an , der einer der häufigsten thermodynamischen Kreisprozessen in Wärmekraftwerken ist. In diesem Fall wird ein einfacher Zyklus ohne Wiedererwärmung und ohne Kondensationsdampfturbine mit Sattdampf (Trockendampf) angenommen. In diesem Fall arbeitet die Turbine im stationären Zustand mit Einlassbedingungen von 6 MPa, t = 275,6 ° C, x = 1 (Punkt 3). Dampf verlässt diese Turbinenstufe mit einem Druck von 0,008 MPa, 41,5 ° C und x = ??? (Punkt 4).
Nehmen wir den Rankine-Zyklus an , der einer der häufigsten thermodynamischen Kreisprozessen in Wärmekraftwerken ist. In diesem Fall wird ein einfacher Zyklus ohne Wiedererwärmung und ohne Kondensationsdampfturbine mit Sattdampf (Trockendampf) angenommen. In diesem Fall arbeitet die Turbine im stationären Zustand mit Einlassbedingungen von 6 MPa, t = 275,6 ° C, x = 1 (Punkt 3). Dampf verlässt diese Turbinenstufe mit einem Druck von 0,008 MPa, 41,5 ° C und x = ??? (Punkt 4).
Berechnung:
- die Dampfqualität des Auslassdampfes
- die Enthalpiedifferenz zwischen diesen beiden Zuständen (3 → 4), die der Arbeit des Dampfes W T entspricht .
- die Enthalpie – Differenz zwischen diesen beiden Zuständen (1 → 2), das entspricht die Arbeit von Pumpen erfolgen, W P .
- die Enthalpiedifferenz zwischen diesen beiden Zuständen (2 → 3), die der im Dampferzeuger zugeführten Nettowärme entspricht
- den thermodynamischen Wirkungsgrad dieses Zyklus und vergleichen Sie diesen Wert mit dem Wirkungsgrad des Carnot
1)
Da wir die genaue Dampfqualität des Auslassdampfes nicht kennen, müssen wir diesen Parameter bestimmen. Der Zustand 4 wird durch den Druck p 4 = 0,008 MPa und die Tatsache festgelegt, dass die spezifische Entropie für die isentrope Expansion konstant ist (s 3 = s 4 = 5,89 kJ / kgK für 6 MPa ). Die spezifische Entropie von gesättigtem flüssigem Wasser (x = 0) und trockenem Dampf (x = 1) kann aus Dampftabellen entnommen werden . Bei feuchtem Dampf kann die tatsächliche Entropie mit der Dampfqualität x und den spezifischen Entropien von gesättigtem flüssigem Wasser und trockenem Dampf berechnet werden:
s 4 = s v x + (1 – x) s l
wo
s 4 = Entropie des feuchten Dampfes (J / kg K) = 5,89 kJ / kgK
s v = Entropie von “trockenem” Dampf (J / kg K) = 8,227 kJ / kg K (für 0,008 MPa)
s l = Entropie von gesättigtem flüssigem Wasser (J / kg K) = 0,592 kJ / kg K (für 0,008 MPa)
Aus dieser Gleichung ergibt sich folgende Dampfqualität:
x 4 = ( s 4 – s l ) / ( s v – s l ) = (5,89 – 0,592) / (8,227 – 0,592) = 0,694 = 69,4%
2)
Die Enthalpie für den Zustand 3 kann direkt aus den Dampftabellen entnommen werden, während die Enthalpie für den Zustand 4 anhand der Dampfqualität berechnet werden muss:
h 3, v = 2785 kJ / kg
h 4, nass = h 4, v x + (1 – x) h 4, l = 2576. 0,694 + (1 – 0,694). 174 = 1787 + 53,2 = 1840 kJ / kg
Dann wird die Arbeit durch den Dampf gemacht, W T, ist
W T = Δh = 945 kJ / kg
3)
Die Enthalpie für Zustand 1 kann direkt aus den Dampftabellen entnommen werden:
h 1, l = 174 kJ / kg
Der Zustand 2 wird durch den Druck p 2 = 6,0 MPa und die Tatsache festgelegt, dass die spezifische Entropie für die isentrope Kompression konstant ist (s 1 = s 2 = 0,592 kJ / kgK für 0,008 MPa ). Für diese Entropie s 2 = 0,592 kJ / kgK und p 2 = 6,0 MPa finden wir h 2, unterkühlt in Dampftabellen für Druckwasser (unter Verwendung der Interpolation zwischen zwei Zuständen).
h 2, unterkühlt = 179,7 kJ / kg
Dann erfolgt die Arbeit der Pumpen, W P, ist
W P = Δh = 5,7 kJ / kg
4)
Die Enthalpiedifferenz zwischen (2 → 3), die der im Dampferzeuger zugeführten Nettowärme entspricht, beträgt einfach:
Q add = h 3, v – h 2, unterkühlt = 2785 – 179,7 = 2605,3 kJ / kg
Beachten Sie, dass in diesem Zyklus keine Wärmerückgewinnung stattfindet. Andererseits ist der größte Teil der zugeführten Wärme für die Verdampfungsenthalpie (dh für den Phasenwechsel) bestimmt.
5)
In diesem Fall bilden Dampferzeuger, Dampfturbinen, Kondensatoren und Speisewasserpumpen eine Wärmekraftmaschine, die den durch den zweiten Hauptsatz der Thermodynamik auferlegten Effizienzbeschränkungen unterliegt . Im Idealfall (keine Reibung, reversible Prozesse, perfektes Design) hätte diese Wärmekraftmaschine einen Carnot-Wirkungsgrad von
η Carnot = 1 – T kalt / T heiß = 1 – 315/549 = 42,6%
Wenn die Temperatur des heißen Reservoirs 275,6 ° C (548,7 K) beträgt, beträgt die Temperatur des kalten Reservoirs 41,5 ° C (314,7 K).
Der thermodynamische Wirkungsgrad dieses Zyklus kann nach folgender Formel berechnet werden:
somit ist
η th = (945 – 5,7) / 2605,3 = 0,361 = 36,1%
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.