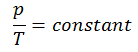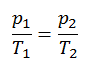Cycle Carnot – diagramme pV, Ts
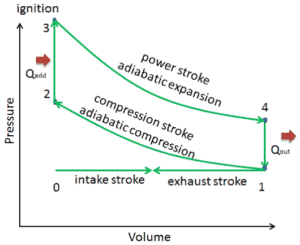
Le cycle d’Otto est souvent tracé sur un diagramme pression-volume (diagramme pV ) et sur un diagramme température-entropie (diagramme Ts). Tracés sur un diagramme de volume de pression, les processus isochoriques suivent les lignes isochoriques du gaz (les lignes verticales), les processus adiabatiques se déplacent entre ces lignes verticales et la zone délimitée par la piste cyclable complète représente le travail total pouvant être effectué pendant une journée. cycle.
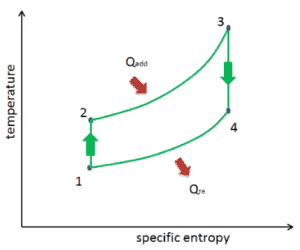
Diagramme température-entropie (diagramme Ts ) dans lequel l’état thermodynamique est spécifié par un point sur un graphique avec une ou des entropies spécifiques comme axe horizontal et une température absolue (T) comme axe vertical. Les diagrammes Ts sont un outil utile et courant, notamment parce qu’il permet de visualiser le transfert de chaleur au cours d’un processus. Pour les processus réversibles (idéaux), l’aire sous la courbe Ts d’un processus est la chaleur transférée au système pendant ce processus.
Processus isentropique
Un processus isentropique est un processus thermodynamique , dans lequel l’ entropie du fluide ou du gaz reste constante. Cela signifie que le processus isentropique est un cas particulier d’un processus adiabatique dans lequel il n’y a pas de transfert de chaleur ou de matière. Il s’agit d’un processus adiabatique réversible . L’hypothèse d’absence de transfert de chaleur est très importante, car nous ne pouvons utiliser l’approximation adiabatique que dans des processus très rapides .
Processus isentropique et première loi
Pour un système fermé, on peut écrire la première loi de la thermodynamique en termes d’enthalpie :
dH = dQ + Vdp
ou
dH = TdS + Vdp
Processus isentropique (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 ) (pour le gaz parfait )
Processus isentropique du gaz parfait
Le processus isentropique (un cas particulier du processus adiabatique) peut être exprimé avec la loi du gaz parfait comme:
pV κ = constant
ou
p 1 V 1 κ = p 2 V 2 κ
dans laquelle κ = c p / c v est le rapport des chaleurs spécifiques (ou capacités calorifiques ) pour le gaz. Un pour une pression constante (c p ) et un pour un volume constant (c v ) . Notez que ce rapport κ = c p / c v est un facteur déterminant la vitesse du son dans un gaz et d’autres processus adiabatiques.
Processus isotherme
Un processus isochore est un processus thermodynamique, dans lequel le volume du système fermé reste constant (V = const). Il décrit le comportement du gaz à l’intérieur du conteneur, qui ne peut pas être déformé. Étant donné que le volume reste constant, le transfert de chaleur dans ou hors du système ne fonctionne pas avec le p∆V , mais modifie uniquement l’ énergie interne (la température) du système.
Processus isochorique et première loi
La forme classique de la première loi de la thermodynamique est l’équation suivante:
dU = dQ – dW
Dans cette équation, dW est égal à dW = pdV et est connu comme le travail aux limites . Alors:
dU = dQ – pdV
Dans le processus isochore et le gaz parfait , toute la chaleur ajoutée au système sera utilisée pour augmenter l’énergie interne.
Processus isochorique (pdV = 0):
dU = dQ (pour le gaz parfait)
dU = 0 = Q – W → W = Q (pour le gaz parfait)
Processus isochorique du gaz parfait
Le processus isochore peut s’exprimer avec la loi du gaz parfait comme:
ou
Sur un diagramme pV , le processus se produit le long d’une ligne horizontale qui a l’équation V = constante.
Voir aussi: Loi de Guy-Lussac
Comparaison des cycles Otto réels et idéaux
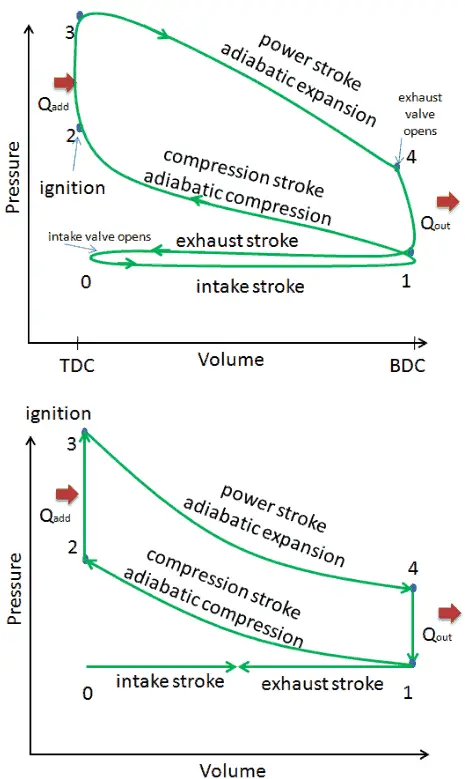Dans cette section, il est montré un cycle Otto idéal dans lequel il y a beaucoup d’ hypothèses différentes du cycle Otto réel . Les principales différences entre le moteur Otto réel et idéal apparaissent sur la figure. En réalité, le cycle idéal ne se produit pas et il y a de nombreuses pertes associées à chaque processus. Pour un cycle réel, la forme du diagramme pV est similaire à l’idéal, mais la zone (travail) entourée par le diagramme pV est toujours inférieure à la valeur idéale. Le cycle Otto idéal est basé sur les hypothèses suivantes:
- Cycle fermé. La plus grande différence entre les deux diagrammes est la simplification des courses d’admission et d’échappement dans le cycle idéal. Dans la course d’échappement, la chaleur Q out est éjectée dans l’environnement, dans un vrai moteur, le gaz quitte le moteur et est remplacé par un nouveau mélange d’air et de carburant.
- Ajout de chaleur instantané (ajout de chaleur isochore). Dans les moteurs réels, l’apport de chaleur n’est pas instantané, donc la pression de pointe n’est pas au PMH, mais juste après le PMH.
- Pas de transfert de chaleur (adiabatique)
- Compression – Le gaz (mélange carburant-air) est comprimé de manière adiabatique de l’état 1 à l’état 2. Dans les moteurs réels, il y a toujours des inefficacités qui réduisent l’efficacité thermique.
- Expansion. Le gaz (mélange carburant-air) se détend adiabatiquement de l’état 3 à l’état 4.
- Combustion complète du mélange air-carburant.
- Aucun travail de pompage . Le travail de pompage est la différence entre le travail effectué pendant la course d’échappement et le travail effectué pendant la course d’admission. Dans les cycles réels, il existe une différence de pression entre les pressions d’échappement et d’entrée.
- Aucune perte de purge . La perte de purge est causée par l’ouverture précoce des soupapes d’échappement. Il en résulte une perte de rendement de travail pendant la course d’expansion.
- Pas de perte par coup . La perte par soufflage est causée par la fuite de gaz comprimés à travers les segments de piston et autres crevasses.
- Pas de pertes par friction .
Ces hypothèses et pertes simplificatrices conduisent au fait que la zone fermée (travail) du diagramme pV pour un moteur réel est significativement plus petite que la taille de la zone (travail) incluse par le diagramme pV du cycle idéal. En d’autres termes, le cycle moteur idéal surestimera le travail net et, si les moteurs tournent à la même vitesse, une plus grande puissance produite par le moteur réel d’environ 20%.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
