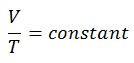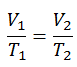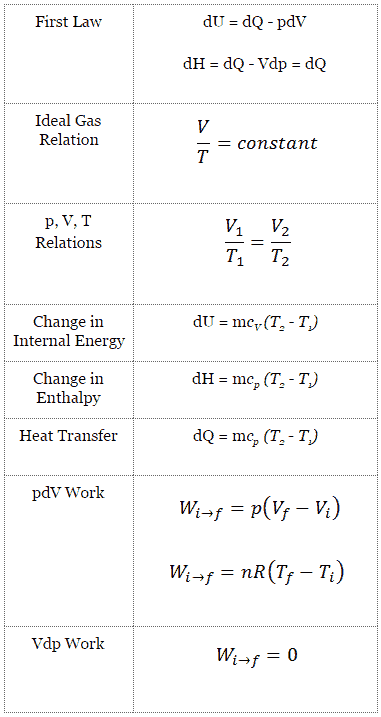Brayton Cycle – Moteur à turbine
En 1872, un ingénieur américain, George Bailey Brayton, a fait progresser l’étude des moteurs thermiques en brevetant un moteur à combustion interne à pression constante, utilisant initialement du gaz vaporisé, puis des combustibles liquides tels que le kérosène. Ce moteur thermique est connu sous le nom de « moteur prêt de Brayton » . Cela signifie que le moteur Brayton d’origine utilisait un compresseur à piston et un détendeur à piston au lieu d’une turbine à gaz et d’un compresseur à gaz.
Aujourd’hui, les moteurs à turbine à gaz et les turboréacteurs modernes à air comprimé sont également des moteurs thermiques à pression constante. C’est pourquoi nous décrivons leur thermodynamique selon le cycle de Brayton . En général, le cycle de Brayton décrit le fonctionnement d’un moteur thermique à pression constante .
C’est l’un des cycles thermodynamiques les plus courants que l’on puisse trouver dans les centrales à turbine à gaz ou dans les avions. Contrairement au cycle de Carnot , le cycle de Brayton n’exécute pas de processus isothermiques , car ceux-ci doivent être effectués très lentement. Dans un cycle de Brayton idéal , le système qui exécute le cycle subit une série de quatre processus: deux processus isentropiques (adiabatiques réversibles) alternés avec deux processus isobares.
Puisque le principe de Carnot stipule qu’aucun moteur ne peut être plus efficace qu’un moteur réversible ( un moteur thermique Carnot ) fonctionnant entre la même température élevée et des réservoirs à basse température, une turbine à gaz en fonction du cycle Brayton doit avoir une efficacité inférieure à l’efficacité Carnot.
Une grande turbine à gaz à cycle unique produit par exemple, par exemple, 300 mégawatts d’énergie électrique et un rendement thermique compris entre 35 et 40%. Les installations modernes à turbine à gaz à cycle combiné (CCGT), dans lesquelles le cycle thermodynamique est constitué de deux cycles de centrale (par exemple, le cycle de Brayton et le cycle de Rankine), peuvent atteindre un rendement thermique d’environ 55%.
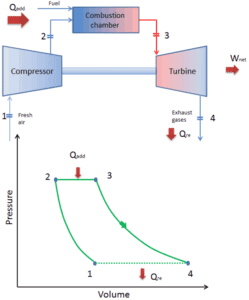
Cycle de Brayton – Processus
Cycle de Brayton – Processus
Dans un cycle de Brayton idéal fermé , le système exécutant le cycle subit une série de quatre processus: deux processus isentropiques (adiabatiques réversibles) alternés avec deux processus isobares:
-
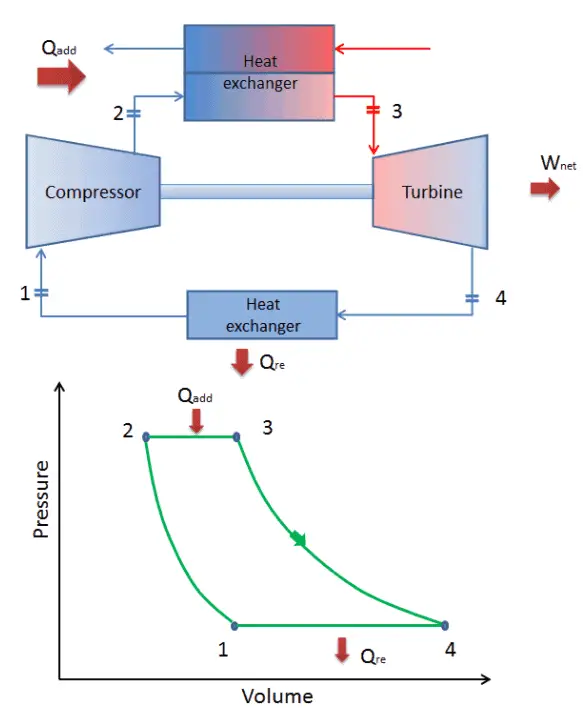
cycle de Brayton fermé Compression isentropique (compression dans un compresseur) – Le gaz de travail (par exemple l’hélium) est comprimé de manière adiabatique de l’état 1 à l’état 2 par le compresseur (généralement un compresseur à flux axial). L’environnement travaille sur le gaz, augmentant son énergie interne (température) et le compressant (augmentant sa pression). En revanche, l’entropie reste inchangée. Le travail requis pour le compresseur est donné par W C = H 2 – H 1 .
- Apport de chaleur isobare (dans un échangeur de chaleur) – Dans cette phase (entre l’état 2 et l’état 3), il y a un transfert de chaleur à pression constante vers le gaz depuis une source externe, car la chambre est ouverte pour entrer et sortir. Dans un cycle de Brayton idéal ouvert, l’air comprimé traverse ensuite une chambre de combustion, où le carburant est brûlé et l’air ou un autre milieu est chauffé (2 → 3). Il s’agit d’un processus à pression constante, car la chambre est ouverte pour entrer et sortir. La chaleur nette ajoutée est donnée par Q add = H 3 – H 2
- Expansion isentropique (expansion dans une turbine) – Le gaz comprimé et chauffé se détend adiabatiquement de l’état 3 à l’état 4 dans une turbine. Le gaz travaille sur l’environnement (pales de la turbine) et perd une quantité d’énergie interne égale au travail qui quitte le système. Le travail effectué par turbine est donné par W T = H 4 – H 3 . Encore une fois, l’entropie reste inchangée.
- Rejet de chaleur isobare (dans un échangeur de chaleur) – Dans cette phase, le cycle se termine par un processus à pression constante dans lequel la chaleur est rejetée du gaz. La température du gaz de travail chute du point 4 au point 1. La chaleur nette rejetée est donnée par Q re = H 4 – H 1
Lors d’un cycle de Brayton, des travaux sont effectués sur le gaz par le compresseur entre les états 1 et 2 ( i compression sentropique ). Le travail est effectué par le gaz dans la turbine entre les étapes 3 et 4 ( i expansion sentropique ). La différence entre le travail effectué par le gaz et le travail effectué sur le gaz est le travail net produit par le cycle et il correspond à l’aire délimitée par la courbe du cycle (en diagramme pV).
Comme on peut le voir, il est commode d’utiliser l’ enthalpie ou l’ enthalpie spécifique et d’exprimer la première loi en termes d’enthalpie dans l’analyse de ce cycle thermodynamique. Cette forme de loi simplifie la description du transfert d’énergie . À pression constante , le changement d’enthalpie est égal à l’ énergie transférée de l’environnement par le chauffage:
Processus isobare (Vdp = 0):
dH = dQ → Q = H 2 – H 1
À entropie constante , c’est-à-dire dans un processus isentropique, le changement d’enthalpie est égal au travail de processus d’écoulement effectué sur ou par le système:
Processus isentropique (dQ = 0):
dH = Vdp → W = H 2 – H 1
Voir aussi: Pourquoi les ingénieurs motoristes utilisent l’enthalpie? Réponse: dH = dQ + Vdp
Processus isentropique
Un processus isentropique est un processus thermodynamique , dans lequel l’ entropie du fluide ou du gaz reste constante. Cela signifie que le processus isentropique est un cas particulier d’un processus adiabatique dans lequel il n’y a pas de transfert de chaleur ou de matière. Il s’agit d’un processus adiabatique réversible . L’hypothèse d’absence de transfert de chaleur est très importante, car nous ne pouvons utiliser l’approximation adiabatique que dans des processus très rapides .
Processus isentropique et première loi
Pour un système fermé, on peut écrire la première loi de la thermodynamique en termes d’enthalpie :
dH = dQ + Vdp
ou
dH = TdS + Vdp
Processus isentropique (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C p (T 2 – T 1 ) (pour le gaz parfait )
Processus isentropique du gaz parfait
Le processus isentropique (un cas particulier du processus adiabatique) peut être exprimé avec la loi du gaz parfait comme:
pV κ = constant
ou
p 1 V 1 κ = p 2 V 2 κ
dans laquelle κ = c p / c v est le rapport des chaleurs spécifiques (ou capacités calorifiques ) pour le gaz. Un pour une pression constante (c p ) et un pour un volume constant (c v ) . Notez que ce rapport κ = c p / c v est un facteur déterminant la vitesse du son dans un gaz et d’autres processus adiabatiques.
Processus isobare
Un processus isobare est un processus thermodynamique , dans lequel la pression du système reste constante (p = const). Le transfert de chaleur dans ou hors du système fonctionne, mais modifie également l’énergie interne du système.
Puisqu’il y a des changements d’ énergie interne (dU) et des changements de volume du système (∆V), les ingénieurs utilisent souvent l’ enthalpie du système, qui est définie comme:
H = U + pV
Processus isobare et première loi
La forme classique de la première loi de la thermodynamique est l’équation suivante:
dU = dQ – dW
Dans cette équation, dW est égal à dW = pdV et est connu comme le travail aux limites . Dans un procédé isobare et le gaz parfait, une partie de la chaleur ajoutée au système sera utilisée pour faire le travail et une partie de la chaleur ajoutée augmentera l’ énergie interne (augmentera la température). Par conséquent, il est commode d’utiliser l’ enthalpie au lieu de l’énergie interne.
Processus isobare (Vdp = 0):
dH = dQ → Q = H 2 – H 1
À entropie constante , c’est-à-dire dans un processus isentropique, le changement d’enthalpie est égal au travail de processus d’écoulement effectué sur ou par le système.
Processus isobare du gaz parfait
Le processus isobare peut s’exprimer avec la loi du gaz parfait comme:
ou
Sur un diagramme pV , le processus se produit le long d’une ligne horizontale (appelée isobare) qui a l’équation p = constante.
Voir aussi: Charles’s Law
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci