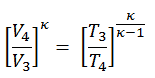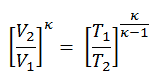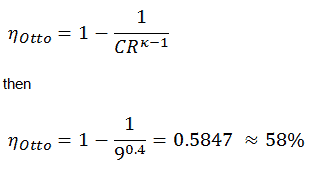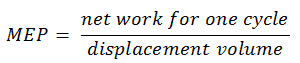Qu’est-ce qu’Otto Cycle – Problème de solution – Définition

Cycle Otto – Problème de solution

Supposons le cycle d’Otto , qui est l’un des cycles thermodynamiques les plus courants que l’on puisse trouver dans les moteurs d’automobiles . L’un des paramètres clés de ces moteurs est la variation des volumes entre le point mort haut (TDC) et le point mort bas (BDC). Le rapport de ces volumes ( V ₁ / V ₂ ) est appelé taux de compression .

Le taux de compression d’un moteur à essence ne sera généralement pas beaucoup plus élevé que 10: 1 en raison du choc potentiel du moteur (auto-allumage) et non inférieur à 6: 1. Par exemple, certains moteurs de voitures de sport peuvent avoir un taux de compression allant jusqu’à 12,5: 1 (par exemple, Ferrari 458 Italia).

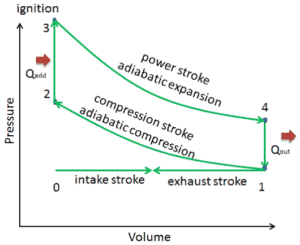
Dans cet exemple, supposons un cycle Otto avec un taux de compression de CR = 9: 1 . L’air aspiré est à 100 kPa = 1 bar, 20 ° C et le volume de la chambre est de 500 cm³ avant la course de compression. La température à la fin de la dilatation adiabatique est T ₄ = 800 K.

• Capacité thermique spécifique à pression constante de l’air à la pression atmosphérique et à la température ambiante: c _p = 1,01 kJ / kgK.
• Capacité thermique spécifique à volume constant d’air à la pression atmosphérique et à la température ambiante: c _v = 0,718 kJ / kgK.
• κ = c _p / c _v = 1,4

Calculer:

1. la masse d’air d’admission
2. la température T ₃
3. la pression p ₃
4. la quantité de chaleur ajoutée par la combustion du mélange air-carburant
5. l’efficacité thermique de ce cycle
6. le député européen

Solution:

1)  la masse d’air d’admission

Au début des calculs, nous devons déterminer la quantité de gaz dans le cylindre avant la course de compression. En utilisant la loi du gaz parfait, nous pouvons trouver la masse:

pV = mR _spécifique T

où:

• p est la pression absolue du gaz
• m est la masse de substance
• T est la température absolue
• V est le volume
• R _spécifique  est la constante de gaz spécifique, égale à la constante de gaz universelle divisée par la masse molaire (M) du gaz ou du mélange. Pour l’air sec R _spécifique = 287,1 J.kg ^-1 .K ^-1 .

par conséquent

m = p ₁ V ₁ / R _spécifique T ₁ = (100000 × 500 × 10 ^-6 ) / (287,1 × 293) = 5,95 × 10 ^-4 kg

Dans ce problème, tous les volumes sont connus:

• V ₁ = V ₄ = V _max = 500 × 10 ^-6 m ³ (0,5 l)
• V ₂ = V ₃ = V _min = V _max / CR = 55,56 × 10 ^-6 m ³

Notez que (V _max – V _min ) x nombre de cylindres = cylindrée totale du moteur.

2)  la température T ₃

Puisque le processus est adiabatique, nous pouvons utiliser la relation p, V, T suivante pour les processus adiabatiques :

Donc

T ₃ = T ₄ . CR ^{κ – 1} = 800. 9 ^0,4 = 1926 K

3)  la pression p ₃

Encore une fois, nous pouvons utiliser la loi du gaz parfait pour trouver la pression au début de la course de puissance comme:

p ₃ = mR _spécifique T ₃ / V ₃ = 5,95 × 10 ^-4 x 287,1 x 1926 / 55,56 × 10 ^-6 = 5920000 Pa = 59,2 bar

4)  la quantité de chaleur ajoutée

Pour calculer la quantité de chaleur ajoutée par la combustion du mélange air-carburant, Q _add , nous devons utiliser la première loi de la thermodynamique pour le processus isochore , qui indique que Q _add = ∆U, donc:

Q _add = mc _v (T ₃ – T ₂ )

la température à la fin de la course de compression peut être déterminée en utilisant la relation p, V, T pour les processus adiabatiques entre les points 1 → 2.

T ₂ = T ₁ . CR ^{κ – 1} = 293. 9 ^0,4 = 706 K

ensuite

Q _add = mc _v (T ₃ – T ₂ ) = 5,95 × 10 ^-4 x 718 x 1220 = 521,2 J

5)  l’efficacité thermique

Efficacité thermique pour un cycle Otto:

Comme dérivé dans la section précédente, l’efficacité thermique d’un cycle d’Otto est fonction du taux de compression et de κ:

6)  la pression moyenne effective

Le député européen a été défini comme:

Si cette équation, le volume de déplacement est égal à V _max – V _min . Le travail net pour un cycle peut être calculé en utilisant la chaleur ajoutée et l’efficacité thermique:

W _net = Q _add . η _Otto = 521,2 x 0,5847 = 304,7 J
MEP = 304,7 / ( 500 × 10 ^-6 – 55,56 × 10 ^-6 ) = 685,6 kPa = 6,856 bar